Условия не достаточно. Вокруг а1b1ab можно описать окружность у которой ab -диаметр. Отрезок а1b1-равен радиусу. Угол a1bb1 равен 30 градусам (половина центрального угла). Если угол abc=сab, то abc равен 60.
Значит угол abc - любой из диапазона (30, 90) градусов.
Угол стремится к 90, когда второй угол стремится к 30, т.е. треугольник становится прямоугольным, а b1a1 его высота к гипотенузе (точки b и b1 совпадают и b1a1 равен ba/2)
Вот если треугольник не просто острый, а равнобедренный, то abc=60 градусам.
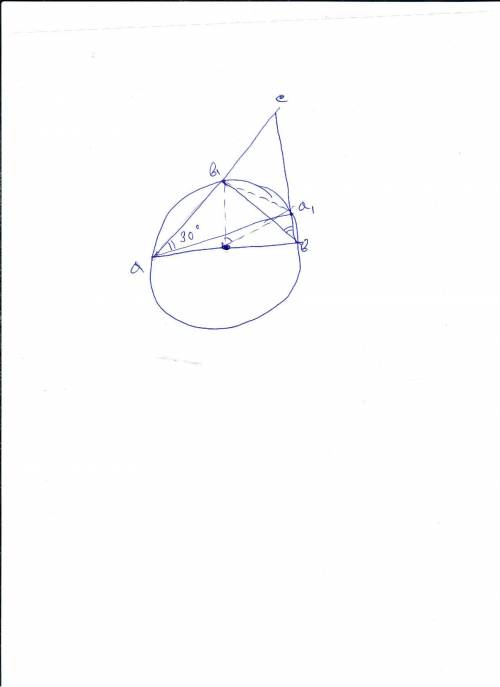
Условия не достаточно. Вокруг а1b1ab можно описать окружность у которой ab -диаметр. Отрезок а1b1-равен радиусу. Угол a1bb1 равен 30 градусам (половина центрального угла). Если угол abc=сab, то abc равен 60.
Значит угол abc - любой из диапазона (30, 90) градусов.
Угол стремится к 90, когда второй угол стремится к 30, т.е. треугольник становится прямоугольным, а b1a1 его высота к гипотенузе (точки b и b1 совпадают и b1a1 равен ba/2)
Вот если треугольник не просто острый, а равнобедренный, то abc=60 градусам.

BC=9
уголВ=30
Проводим высоту AH из угла A на сторону ВС
Тогда площадь равна S=BC*AH/2
Треугольник AHB прямоугольный, AB - гипотенуза, угол B равен 30. Есть такая теорема, что катет, лежащий на против угла в 30 градусов равен половине гипотенузы, значит AH=AB/2=12/2=6
Возвращаемся к площади S=BC*AH/2=9*6/2=27