В научной литературе зафиксировано не менее 400 доказательств теоремы Пифагора, что объясняется как фундаментальным значением для геометрии, так и элементарностью результата. Основные направления доказательств: алгебраическое использование соотношений элементов треугольника (таков, например, популярный метод подобия[⇨]), метод площадей[⇨], существуют также различные экзотические доказательства (например, с дифференциальных уравнений).
Через подобные треугольники
Одним из наиболее популярных в учебной литературе доказательств алгебраической формулировки является доказательство с использованием техники подобия треугольников, при этом оно почти непосредственно выводится из аксиом и не задействует понятие площади фигуры.[10] В нём для треугольника ABC с прямым углом при вершине C со сторонамиa,b,c, противолежащими вершинам A,B,C соответственно, проводится высота при этом согласно признаку подобия по равенству двух углов) возникают соотношения подобия: и , из чего непосредственно следуют соотношения.
При перемножении крайних членов пропорций выводятся равенства:
покомпонентное сложение которых даёт требуемый результат.
(хз надеюсь правильно)
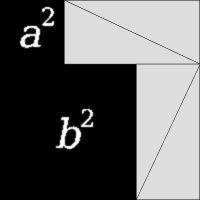
Объяснение:
Первый признак подобия треугольников
Если два угла одного треугольника соответственно равны двум углам другого, то эти треугольники подобны
Второй признак подобия треугольников
Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны
Третий признак подобия треугольников
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
ВОТ ПРАВИЛА : САМА ДУМАЙ АХАХ НО Я ХЗ Я ДУМАЮ ЭТО 1 ПРИЗНАК Х
Площадь полной поверхности конуса - это площадь основания конуса + площадь боковой поверхности.
S(бок) = 2пиrh, h - высота конуса, r - радиус основания конуса.
S(осн) = пиr^2
Нам надо знать для решения этой задачи длины высоты конуса и его радиуса. Конечно же, найдём мы их из прямоугольного треугольника ASO.
cos 60 = AO/AS;
cos 60 = r/8
1/2 = r/8
r = 4 - радиус найден.
В треугольнике ASO по теореме Пифагора находим другой катет - высоту конуса.
h = корень из (8^2 - 4^2) = корень из 48
Теперь легко находим полную поверхность конуса как сумму боковой поверхности и площади основания:
S = 16пи + 8 корней из 48 * пи
Если же <ASO = 60 градусам, то рассмотрим теперь такой вариант, совершенно аналогичный прежнему. Рассмотрим всё тот же прямоугольный треугольник ASO.
Тогда <SAO = 30 градусам, а катет, лежащий против угла в 30 градусам, равен половине гипотенузы. таким образом, SO = 1/2AS = 1/2 * 8 = 4
Находим радиус теперь по теореме Пифагора, он равен корню из 48, это высота конуса. Теперь площадь поверхности находится легко:
S = 48пи + 8корней из 48 пи. ответ на второй случай также получен. Задача решена.