Дано:
NK=KL=LM
уголLNM=30°
Найти: уголК; уголL; уголM; уголN
уголLNM=уголKLN=30°(как накрест лежащие при KL||NM и секущей NL)
Т.к ∆NKL- равнобедренный(по условию), то уголKLN= уголKNL= 30°
Значит, уголN= уголKNL+уголLNM=30°+30°=60°
По свойству равнобедренной трапеции уголМ=уголN=60°
По свойству трапеции:
уголN+уголК=180°
уголК=180°-уголN=180°-60°= 120°; и
уголМ+уголL=180°
уголL=180°-уголМ=180°-60°= 120°
УголК=уголL(как углы при основании равнобедренной трапеции)
ответ: уголК=120°; уголL=120°; уголМ=60°; уголN=60°
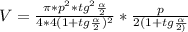 =
=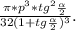
Полученный теуг-к АМВ- прямоугольный (Угол АМВ=90). Угол АВМ является смежным данному углу АВС, значит АВМ=180-120=60. Угол МАВ=180-(60+90)=30. А в прямоугольном треуг-ке катет, лежащий против угла 30 градусов равен половине гипотенузы, значит, ВМ=1/2АВ=1/2 *18=9
ответ: ВМ=9см.