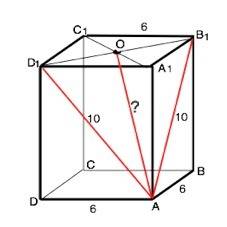
А1С1 – диагональ квадрата со стороной, равной 6 см
Формула диагонали квадрата d=a√2 ⇒
A1C1=6√2
B1D1=A1C1=6√2
Проведем в боковых гранях диагонали AD1 и АВ1
Боковые ребра параллелепипеда равны, основание – квадрат по условию ⇒
треугольник В1АD1 равнобедренный, т.к. диагонали равных граней равны. Диагонали квадрата равны и точкой пересечения делятся пополам. OB1=OD1=3√2
О - центр А1С1. ⇒
АО - медиана ∆ D1AB1. По т.Пифагора из треугольника АОВ1 найдем длину искомого отрезка
АО=√(AB1*-ОВ1*)=√(100-18)=√82
тогда внутренний угол при вершине N равен 180-150. =30
высота, проведенная к стороне MN - KK1
треугольник NKK1 - Прямоугольный
KK1 = NK*sinN
KK1 = 18 * sin 30 = 18 * 1/2 = 9
ответ 9