Объяснение:
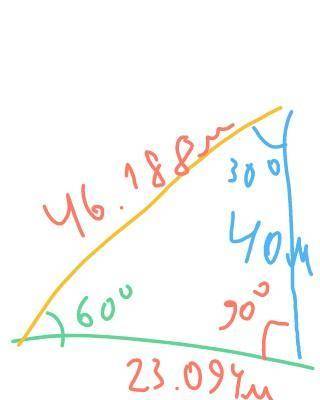
Вот рисунок, по нему решаем задачу
Видно я так понимаю самую верхушку башни под углом в 60°
Слева точка К, просто не подписал
Тогда получается прямоугольный треугольник, угол К равен 60°, правая сторона равна 40 метров
Правый верхний угол равен 30°, а сторона, лежащая напротив него равна половине гипотенузы (sin 30°=0.5)
По теореме Пифагора:
(2х)²=х²+40²
4х²-х²=1600
3х²=1600
х²=533.33
х≈23.094 - это по прямой до основания башни (зеленая линия)
23.094*2=46.188 метров - это до верхушки (желтая линия)
Проверка:
46.188²=23.094²+40²
2133.3333=533.3333+1600 - верно
в треугольнике AHB угол AHB = 90 градусов ==>
сумма углов НАВ + НВА = 90 градусов
cos(BAH) = cos(90 - НВА) = sin(HBA)
основное тригонометрическое тождество (sina)^2 + (cosa)^2 = 1
позволяет найти синус, если известен косинус...
(sin(CBA))^2 = 1 - 4*6/25 = 1/25
sin(CBA) = 1/5 (углы в треугольнике < 180 градусов => синусы этих углов > 0 )))
ответ: 1/5 = 0.2