Периметр параллелограмма равен 50,а длины его высот относятся как 2: 3.найдите длину меньшей стороны параллелограмма.

👇

Ответ:

Fulin666

29.08.2021

А-1сторона,х-высота, опущенная на эту сторону, S=ax
в-2 сторона,у-высота, опущенная на эту сторону, S=ву
ах=ву⇒а/в=у/х
Р=50⇒а+в=25, а=25-в
25-в/в=у/х=3/2
(25-в)*2=3в
50-2в=3в
5в=50⇒в=10
а=25-10=15
ответ меньшая сторона равна 10

4,5(77 оценок)

Открыть все ответы

Ответ:

katya8631

29.08.2021

A1.

Sшестиугольника = 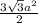$\frac{3\sqrt{3} a^2}{2}$

ответ: 4

A2.

Правильный четырёхугольник - это квадрат. Так как он вписан в окружность, то диаметр окружности будет равен диагонали квадрата. Диагонали квадрата пересекаются в центре и делят его на 4 одинаковых прямоугольных равнобедренных треугольника с бок. сторонами = R ⇒ S квадрата равна площади четырех треугольников:

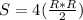
$S = 4 (\frac{R * R}{2} )$ = 2 R^2

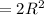
ответ: 1

A3.

Правильный шестиугольник состоит из 6 равносторонних треугольников, стороны которых равны a, а высоты равны радиусу R. Найдем, чему равны стороны через высоту (радиус):

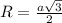
$R = \frac{a\sqrt{3} }{2}$

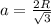
$a = \frac{2R}{\sqrt{3}}$

Площадь одного треугольника будет равна:

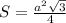
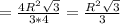
$S = \frac{a^2\sqrt{3} }{4}$ $= \frac{4R^2\sqrt{3} }{3*4} = \frac{R^2\sqrt{3}}{3 }$

Площадь шестиугольника:

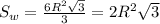
$S_w = \frac{6R^2\sqrt{3} }{3} = 2R^2\sqrt{3}$

ответ: 2

B1.

Пусть вписанный треугольник - ΔABC, сторона = ; описанный - ΔA₁B₁C₁, сторона - a_1

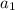
Для ΔA₁B₁C₁ радиус 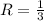$R = \frac{1}{3}$ высоты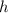

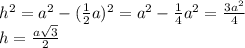
$h^2 = a^2 - (\frac{1}{2} a)^2 = a^2 - \frac{1}{4} a^2 = \frac{3a^2}{4} \\h = \frac{a\sqrt{3} }{2}$

$R = \frac{a\sqrt{3} }{2} * \frac{1}{3} = \frac{a\sqrt{3} }{6}$ ⇒

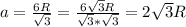
⇒ $a = \frac{6R}{\sqrt{3} } = \frac{6\sqrt{3}R}{\sqrt{3}*\sqrt{3}} = 2\sqrt{3}R$

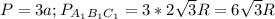
$P = 3a; P_{A_1B_1C_1} = 3 * 2\sqrt{3} R = 6\sqrt{3} R$

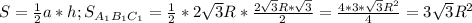
$S = \frac{1}{2} a*h; S_{A_1B_1C_1} = \frac{1}{2} * 2\sqrt{3} R * \frac{2\sqrt{3} R * \sqrt{3} }{2} = \frac{4*3*\sqrt{3} R^2}{4} = 3\sqrt{3} R^2}$

Для ΔABC радиус R = 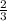$\frac{2}{3}$ высоты :

$R = \frac{a\sqrt{3} }{2} * \frac{2}{3} = \frac{a\sqrt{3} }{3}$ ⇒

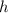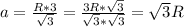
⇒ $a = \frac{R * 3}{\sqrt{3} } = \frac{3R * \sqrt{3} }{\sqrt{3} * \sqrt{3} } = \sqrt{3} R$

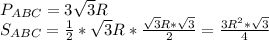
$P_{ABC} = 3\sqrt{3} R\\S_{ABC} = \frac{1}{2} * \sqrt{3} R * \frac{\sqrt{3}R*\sqrt{3}}{2} = \frac{3R^2 * \sqrt{3}}{4}$

Найдем соотношение периметров и площадей:

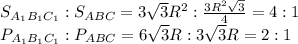
$S_{A_1B_1C_1} : S_{ABC} = 3\sqrt{3}R^2 : \frac{3R^2\sqrt{3} }{4} = 4: 1\\P_{A_1B_1C_1} : P_{ABC} = 6\sqrt{3}R : 3\sqrt{3}R = 2 : 1$

4,6(89 оценок)

Ответ:

орлыварив

29.08.2021

Для доказательства используем теорему о трилистнике, которая гласит, что если биссектриса угла А треугольника АВС пересекает окружность в точке Y и точка I - центр вписанной в ΔАВС окружности, то YB=YI=YC.

Обозначим углы ВАI и САI как α, а углы АВI и СВI как β.
Вписанные углы YAС и YBС равны α т.к. опираются на одну дугу.
∠BIY - внешний треугольника АВI, значит ∠BIY=∠ВAI+∠АВI=α+β.
В треугольнике ВYI ∠YВI=∠BIY=α+β, значит он равнобедренный. YB=YI.
∠ВYX=∠AYX так как они опираются на равные дуги ВХ и АХ, значит YX - биссектриса равнобедренного тр-ка ВYI, значит YX⊥BI и BO=OI.
Треугольники КВО и LBO равны так как ВО - общая сторона и прилежащие к ней углы β и 90° равны, значит КО=ОL.

В четырёхугольнике ВKIL диагонали пересекаются под прямым углом и точкой пересечения делятся пополам, значит ВKIL - ромб.
Доказано.
По : треугольник abc вписан в окружность. точка x - середина дуги ab, не содержащей вершину c, а точ