5 корней из 2-бок,6-основание,7 -площадь
Объяснение:
основные моменты:
0)трапеция вписанная, а значит равнобедренная
1)проведи диаметр АО, соедини его конец с D. в образовавшемся прямоугольном (опирается на диаметр) треугольнике стороны 6, 8 и 10 (египетский)
2)2 вписанных угла, опирающихся на 1 дугу равны, найди 2 подобных по двум углам прямоугольных треугольника. Из подобия легко ищется боковая сторона
3)нижние отрезки диагоналей (AO и DO, если точка пересечений диагоналей О, равны 4 корня из 2 по "теореме Пифагора" или по легкой формуле для равнобедренного прямоугольного)
4) по теореме Пифагора ищем верхние отрезки диагоналей
5)по теореме Пифагора находим ВD
6)высоту находим, проведя ее из В по теореме Пифагора (нижний отрезок на АD равен 1, т.к. трапеция равнобедренная) По высоте находим площадь
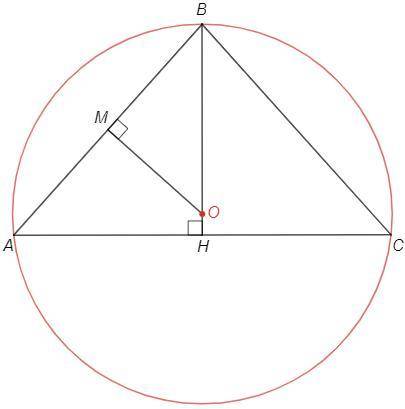
В равнобедренном треугольнике высота к основанию является также биссектрисой и медианой.
BH - высота/биссектриса/медиана
AC=4x, AB=3x
AH =AC/2 =2x
BH =√(AB^2 -AH^2) =√(9-4) x =√5 x (т Пифагора)
Центр вписанной окружности - пересечение биссектрис.
AI - биссектриса
По теореме о биссектрисе
BI/IH =AB/AH =3/2 => IH =2/5 BH =8 (см)
Центр описанной окружности - пересечение серединных перпендикуляров.
MO - серединный перпендикуляр к AB
AB/BH =3/√5 => AB =3/√5 BH =12√5
△OBM~△ABH (прямоугольные с общим углом)
OB/AB =BM/BH => OB/12√5 =6√5/20 => OB =18 (см)
Или
cosA =2/3
sinC =sinA =√(1 -cosA^2) =√5/3
AB =BH/sinA
AB/sinC =2R (т синусов) => R =BH/2sinA^2 =20/2 :(5/9) =18 (см)

y^9 = (y^3)^3 --- при возведении в степень показатели степеней умножаются...
z^27 = (z^9)^3 --- по той же причине...
A = (5 * x * y^3 * z^9)^3