* * * * * * * * * * * * * * * * * * * * * * * * *
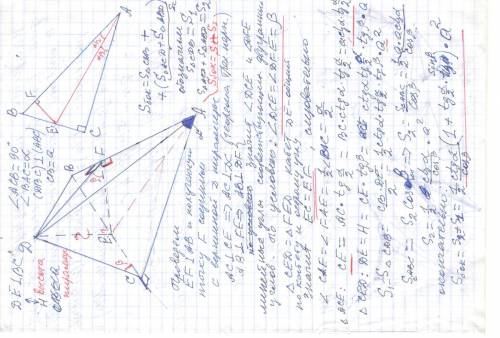
Основание пирамиды – прямоугольный треугольник с катетом а и противолежащим углом α. Боковая грань, содержащая данный катет, перпендикулярна плоскости основания, а две другие наклонены к ней под углом β. Найдите высоту (H) пирамиды и площадь боковой поверхности (Sбок).
Дано : ∠ACB =90° ; CB = a ;
( DCB) ⊥ (ABC) ; (DAC) ^ (ABC) = (DAB) ^ (ABC) = β
- - - - - - -
DE = H -? Sбок - ?
ответ : H=ctgα*tg(α/2)*tgβ , Sбок = 0,5*сtgα/cosβ (1+tg(α/2)*sinβ )*a²


Решение ........ во вложении
центральный угол AOC =2*ABC =2*30 =60
тогда треугольник AOC - равносторонний
тогда хорда АС=R
d=15дм , тогда R =15 дм/2 = 7,5 дм
тогда хорда АС =7,5 дм