Основание прямой призмы равнобедренный треугольник,в котором биссектриса угла при вершине равна 12 см.диагональ боковой грани,содержащей основание треугольника,равна 10 из под корня 2 см. и образует с боковым ребром призмы угол 45.найдите боковое ребро призмы и площадь основания.

👇

Увидеть ответ

Ответ:

PeaceDuck1337

28.02.2022

Обозначим призму АВСС₁В₁А₁.

Основание АС равнобедренного треугольника АВС содержится в грани АА₁С₁С.

Т.к. призма прямая и угол СА₁А=45°, то прямоугольный треугольник АА₁С - равнобедренный, АА₁=АС.

АА₁=АС=А₁С•sin 45º=10√2•(√2/2)=10 см

В равнобедренном треугольнике биссектриса угла при вершине является медианой и высотой.

S ∆ АВС=ВН•AC:2=12•10:2=60 см²

Основание прямой призмы равнобедренный треугольник,в котором биссектриса угла при вершине равна 12 с

4,6(100 оценок)

Открыть все ответы

Ответ:

hide2

28.02.2022

12 см

Объяснение:

1) Острый угол, составляющий 2/3 прямого угла, равен:

90 · 2/3 = 60°.

2) Второй острый угол прямоугольного треугольника равен:

180 - 90 - 60 = 30°.

3) Меньший катет лежит против меньшего угла, то есть против угла 30°.

Катет, лежащий против угла 30°, равен половине гипотенузы.

Пусть х - меньший катет прямоугольного треугольника, тогда гипотенуза равна 2х. Составим уравнение и найдём х:

х + 2х = 18

3х = 18

х = 18 : 3 = 6 см - это длина меньшего катета.

4) Находим длину гипотенузы:

6 · 2 = 12 см

ответ: 12 см

4,8(100 оценок)

Ответ:

nurbibisaidova3

28.02.2022

>>> идёт оформление рисунка <<< ожидайте ...

Задача решается через векторы.
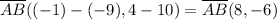Построим вектор $\overline{AB} ( (-1)-(-9) , 4-10 ) = \overline{AB} ( 8 , -6 )$ ;

Середина D отрезка AB может быть найдена откладыванием половины вектора $\overline{AB}$ от точки A

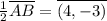$\frac{1}{2} \overline{AB} = \overline{ ( 4 , -3 ) }$ ;

Итак D( -9+4, 10-3 ) = D( -5, 7 ) ;

От точки D нужно отложить вектор высоты $\overline{h}$ в обе возможные стороны

Вектор высоты $\overline{h}$ перпендикулярен вектору основания $\overline{AB}$ , а значит его проекции накрест-пропорциональны с противоположным знаком:

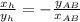(I) $\frac{x_h}{y_h} = -\frac{ y_{AB} }{ x_{AB} }$ , что непосредственно следует из скалярного произведения, поскольку для перпендикулярных векторов должно выполняться: $x_h * x_{AB} + y_h * x_{AB} = 0$ (II) ;

Таким образом вектор $\overline{h}$ пропорционален вектору $\overline{h_o} ( 3 , 4 )$ , поскольку для вектора $\overline{h_o}$ выполняется и равенство (I) и равенство (II) осталось лишь найти масштаб вектора $\overline{h}$ ;

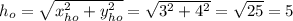Вектор $\overline{h_o}$ имеет длину $h_o = \sqrt{ x_{ho}^2 + y_{ho}^2 } = \sqrt{ 3^2 + 4^2 } = \sqrt{ 25 } = 5$ ;

Аналогично, AB = 10

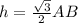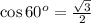При этом, поскольу треугольник равносторонний, то значит его высота составляет $h = \frac{ \sqrt{3} }{2}AB$ , т.к $\cos{ 60^o } = \frac{ \sqrt{3} }{2}$ ;

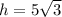Значит $h = 5 \sqrt{3}$ , а стало быть $h = \sqrt{3} h_o$ ;

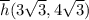В итоге $\overline{h} ( 3\sqrt{3} , 4\sqrt{3} )$ .

Откладываем этот вектор в разные стороны (+\-) от точки D( -5, 7 ) и получаем:

ОТВЕТ:

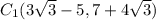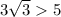$C_1 ( 3\sqrt{3} - 5 , 7 + 4\sqrt{3} )$ /// примечание: $3\sqrt{3} 5$ ;

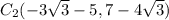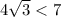$C_2 ( - 3\sqrt{3} -5 , 7 - 4\sqrt{3} )$ /// примечание: $4\sqrt{3} < 7$ .

Вычислить координаты вершины с равностороннего треугольника авс, если даны координаты а(-9,10), в(-1