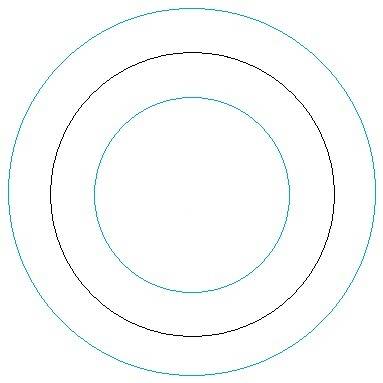
1) Пусть точка M лежит вне окружности. O - центр окружности, точка T - пересечение отрезка OM и окружности. Возьмем на окружности точку T1, не лежащую на OM. В треугольнике MT1O сторона OM меньше суммы двух других сторон (неравенство треугольника),
MT+OT<MT1+OT1 <=> MT<MT1 (OT=OT1, радиусы)
Таким образом, чтобы длина MT была минимальной, T должна лежать на OM. Если M вне окружности, MT=1, OT=2000, то OM=MT+OT=2001. Искомое ГМТ - окружность радиусом 2001 с центром данной окружности.
2) Аналогично доказывается, что если точка M лежит внутри окружности, то искомое ГМТ - окружность радиусом 1999 (OM=OT-MT) с центром данной окружности.

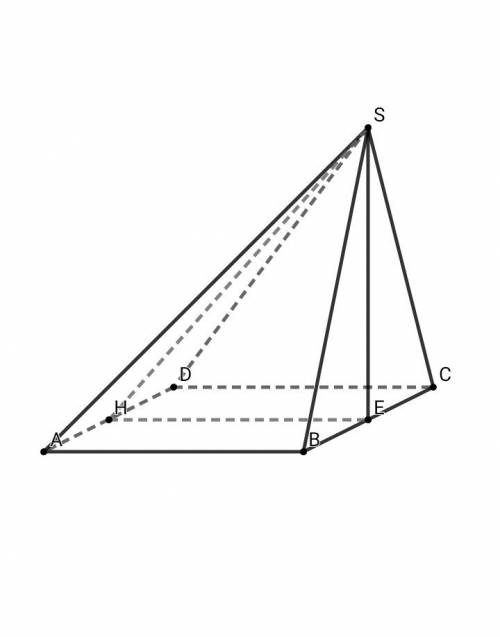
Равные наклонные имеют равные проекции.
Пусть О- проекция точки D.
ОА=ОВ=ОС.
Значит О- центр описанной окружности.
ОА=ОВ=ОС=R
Радиус окружности, описанной около треугольника, находится по формуле
R=abc/4S
a=b=c=12
S=a·a·sin60°/2=a²√3/4
R=a√3/3=12√3/3=4√3 см
∠DAO=∠DBO=∠DCO=45°
Треугольник DАО- прямоугольный равнобедренный
АО=DO=4√3
По теореме Пифагора
DA=4√6.
О т в е т. 4√6 см