Объяснение:
Дано:
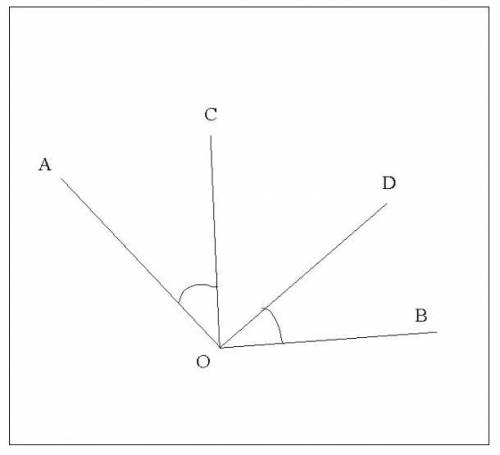
<AOB и <COD
<COD внутри <AOB
AO ┴ OD; CO ┴ OB;
<AOB - <COD = 90°
Найти: <AOB и <COD.
Решение
Т.к . AO ┴ OD; CO ┴ OB,
то <AOD = 90; <COB = 90°.
<COD = <AOD - <AOC
<COD = <COB - <DOB
<COD = 90° - <AOC
<COD = 90° - <DOB
Получим
<AOC = 90° - <COD
<DOB = 90° - <COD
Следовательно <AOC = <DOB
2) По условию: <AOB - <COD = 90°
Но если от всего угла <AOB отнять <COD, то останутся два равных угла <AOC и <DOB, значит, это их сумма равна 90°.
<AOC + <DOB = 90° =>
<AOC = <DOB = 90°/2 = 45°
3) <COD = 90° - <DOB
<COD = 90° - 45°=45°
4) <AOB = <AOC + <DOB + <DOB
<AOB = 45° + 45° + 45° = 135°
ответ: <AOB - 135°; <COD =45°.
ответ:Треугольник АВС равнобедренный,т к по условию АВ=ВС
Если внешний угол равен 80 градусов,то смежный ему внутренний угол равен
180-80=109 градусов равен <В
Углы при основании равнобедренного треугольника равны между собой,поэтому каждый из углов при основании равен
(180-100):2=40 градусов
Номер 2
Внешний угол треугольника равен 140 градусов,а это означает,что два внутренние не смежные с ним угла в сумме равны градусной мере внешнего не смежного с ними угла
3+4=7
Чему равна 1 часть
140:7=20 градусов
Один угол
20•3=60 градусов
Второй угол
20•4=80 градусов
Третий угол
180-140=40 градусов
Номер 3
Первое-биссектрисы поделили углы А и В на 4 равных угла
Второе-треугольник ADB является равнобедренным,т к углы при основании равны между собой и равны
(180-100):2=40 градусов
Угол 40 градусов равен половине угла А
<А=40•2=80 градусов
<А=<В=80 градусов
Угол С равен
180-(80+80)=20 градусов
Объяснение:
В прямоугольном ΔВСД с гипотенузой 20 (диагональ) и углом 61, катет прилежащий углу 61, равен ВС =ВД * сos 61 = 10 * сos 61
В прямоугольном Δ с гипотенузой ВС = 10 * сos 61 и углом 61, противолежащий катет = BC * sin 61 = 10 * сos 61 * sin 61 - искомое расстояние