Основания трапеции параллельны, диагонали трапеции - секущие и при пересечении с ними образуют равные накрестлежащие углы.
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны. ⇒
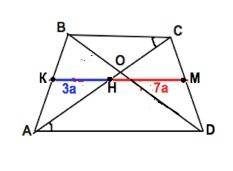
∆ ВОС ~∆ АОD по 1 признаку подобия.
СО:ОА=3:7=> ВС:АD=3:7
КН - средняя линия ∆ АВС.
НМ - средняя линия ∆ САD
Отношения сходственных элементов подобных фигур равны. =>
КН:НМ=3:7
КН+НМ=10 частей
10:10=1 см - длина каждой из 10 частей.
КН=3•1=3 см => BС=2•КН=6 см
НМ=7•1=7 см
АD=2•7=14 см
1)
Биссектриса угла треугольника делит противоположную сторону в отношении, равном отношению сторон, между которыми проведена.
СD:AD=CB:AB
9/6=CB/8⇒
CB=72/6=12 см
Р=АВ+ВС+АС=8+12+(9+6)=35 см
2)
Рисунок к задаче такой же, как к первой.
Найдем третью сторону треугольника:
40-(15+9)=16 см
Биссектриса делит сторону, которую пересекает, на отрезки в отношении 9:15
Примем один отрезок равным х. Тогда другой 16-х
х:(16-х)=9:15 ⇒
24х=144
х=6 см
16-х=10
ответ: 6 см и 10 см