ответ: АР=8
Объяснение (подробно):
ТР - биссектриса ⇒ ∠КТР=∠РТМ.
Т.к. около четырехугольника описана окружность, все углы, вершины которых лежат на ней, -вписанные. Вписанные углы, которые опираются на одну дугу, равны; равны и хорды, которые стягивают равные дуги.
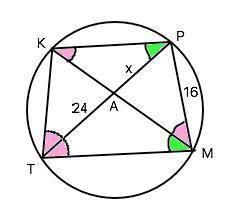
Угол РМК опирается на дугу РК, и угол КТР опираются на дугу КР, следовательно они равны. Но им равен и угол РТМ , следовательно, равны хорды КР=РМ=16.
Примем АР=х. Тогда ТР=ТА+х=24+х
Рассмотрим ∆ ТКР и АКР. Они имеют по два равных угла, следовательно, подобны. Из их подобия следует отношение ТР:КР=КР:АР ⇒
(24+х):16=16:х
Из пропорции получаем 14х+х²=256 ⇒ х²+24х-256. Решив квадратное уравнение находим х₁=8; х₂=-32 ( не подходит).
АР=х=8.
a; b; c; - прямые 1) a и b - параллельные прямые, а с -.
c пересекает a = A секущая. По теореме о пересечении параллельных
c пересекает b = B прямых и секущей, внутренние односторонние углы
угол A : углу В = 2 : 3 в сумме равны
угол А односторонний углу В угол А + угол В =
________________________ 2) Угол А : углу В = 2 : 3, следовательно угол
Найти а) угол А - ?
б) угол В - ? 3)
4)
5)
ответ: а) угол А = 72 градусам
б) угол В = 108 градусам