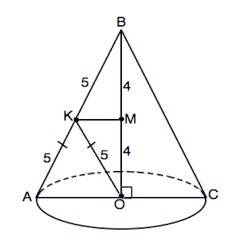
Осевое сечение конуса- равнобедренный треугольник АВС.
Расстояние от центра основания конуса до середины образующей является медианой ОК прямоугольного треугольника АВО, где ВО - высота конуса, АО - радиус основания, АВ- образующая.
Медиана прямоугольного треугольника, проведенная к гипотенузе, равна ее половине.
Следовательно, АВ=2•КО=10 см.
Отношение катета ВО к гипотенузе АВ равно 8:10=4:5, т.е. ∆ АВО египетский, следовательно,
радиус основания конуса АО=6 см ( можно проверить по т.Пифагора с тем же результатом).
1. Вспомним свойство катета: если катет лежит напротив угла в 30°, то он равен половине гипотенузы. Проверим: допустим, катет "AB" лежит напротив угла "D" в 30° и равняется половине гипотенузы "DB". Если мы гипотенузу "DB" поделим пополам, то получим величину катета "AB". Значит угол "D" будет равняться ровно 30°.
2. Так как треугольник "DAB" прямоугольный, то один из углов обязательно должен градусную меру в 90°. Пусть это будет угол "A".
3. Вспомним теорему о сумме углов треугольника: сумма углов равна 180°. То есть мы сможем найти последний угол "B" треугольника "BAD", если вычтим из 180° сумму двух найденных углов (см пункты "1" и "2"). Соответственно угол "B" будет равняться 180°-(90°+30°)=180°-120°=60°.
ответ: 30°, 60°, 90°.
Так как ЕF биссектриса, то угол DEF=30 гр.
Поскольку в равнобедренном треугольнике углы при основании равны, то треугольник DEF равнобедренный.
2)Рассмотрим прямоугольный треугольник CEF. Так как против угла в 30 гр. лежит сторона равная половине гипотенузы, то СF=1/2ЕF.
Так как ЕF=DF, то СF=1/2DF.