Украинский:
трикутник АВС, кут = 90, ВС - гіпотенуза, АН-висота на ВС, ВН = 28, СН = 7
ВН / АН = АН / НС. 28 / АН = АН / 7, АН в квадраті = 196, АН = 14
АС = корінь (АН в квадраті + НС в квадраті) = корінь (196 + 49) = корень245 = 7 х корень5
АВ = корінь (АН в квадраті + ВН в квадраті) = корінь (196 + 784) = корень980 =
= 14 х корень5
Площа = 1/2 х АС х АВ = 1/2 х 7 х корень5 х 14 х корень5 = 245
Русский:
треугольник АВс, уголА=90, ВС - гипотенуза, АН-высота на ВС, ВН=28, СН=7
ВН/АН=АН/НС. 28/АН=АН/7, АН в квадрате = 196, АН=14
АС = корень(АН в квадрате + НС в квадрате) = корень(196 + 49) =корень245 =7 х корень5
АВ = корень (АН в квадрате + ВН в квадрате) = корень(196 + 784) = корень980 =
=14 х корень5
Площадь = 1/2 х АС х АВ = 1/2 х 7 х корень5 х 14 х корень5 = 245
Для даної задачі треба скористатися властивостями катетів та їх проекцій на гіпотенузу в прямокутному трикутнику.
Перший б
Катет прямокутного трикутника — середнє пропорційне між гіпотенузою  і проекцією цього катета на гіпотенузу:
і проекцією цього катета на гіпотенузу:
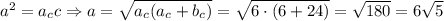 см
см
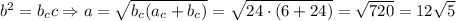 см
см
Площа 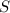 прямокутного трикутника знаходится як півдобуток його катетів:
прямокутного трикутника знаходится як півдобуток його катетів:
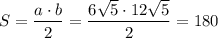 см²
см²
Другий б
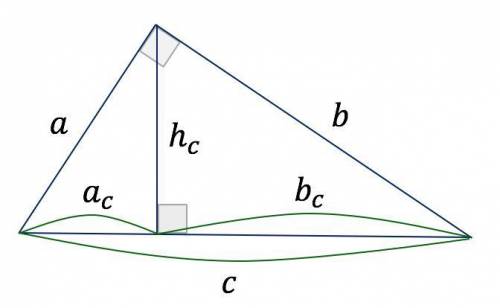
Висота 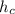 прямокутного трикутника, що проведена до гіпотенузи
прямокутного трикутника, що проведена до гіпотенузи  з вершини прямого кута, — середнє пропорційне між проекціями катетів на гіпотенузу:
з вершини прямого кута, — середнє пропорційне між проекціями катетів на гіпотенузу:
 см
см
Площа 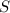 будь-якого трикутника знаходиться як півдобуток його сторони на висоту, що проведена до цієї сторони. У нашому випадку — це півдобуток гіпотенузи
будь-якого трикутника знаходиться як півдобуток його сторони на висоту, що проведена до цієї сторони. У нашому випадку — це півдобуток гіпотенузи  і висоти
і висоти 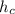 , що до неї проведена:
, що до неї проведена:
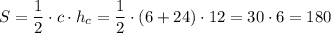 см²
см²
Відповідь: 180 см².
2.Это надо провести на уровне 3 м от земли горизонтальную прямую до второго столба, и получится прямоугольный треугольник с гипотенузой 5 и катетом 6 - 3 = 3.Второй катет и есть расстояние между столбами. Он равен 4. Опять получился египетский треугольник со сторонами 3,4,5...
3.Прямая АВ, точка С. Рисуем треугольник АВС
АВ = 17 см
CB = 15 см
Опускаем высоту СК на сторону АВ. Обозначим
АК = х
КВ = х-4
По теореме Пифагора
CK^2 = AC^2 - AK^2 = CB^2 - KB^2
17^2 - x^2 = 15^2 - (x-4)^2
289 - x^2 = 225 - x^2 + 8x - 16
8x = 80
x = 10
х-4 = 6
4. По заданию треугольник равносторонний т. е AB=AC=BC=8 дм.
Угол от прямой AD к пл-ти треугольника: /_DAC = /_DAB = /_DAM = 90* - (ПО ЗАДАНИЮ ПЕРПЕНДИКУЛЯР)
Далее по теореме Пифагора ( /_ AMC = 90*); MC= BC/2; AM = sqrt( AC2 - MC2)= sqrt (8 - 4) = 6.928 дм.
- точка M лежит на прямой BC. Вобщем AM - медиана и высота выпущенная из точки А и делящая сторону BC пополам.
Расстояние от D до BC: DM= sqrt (AD2 + AM2)= sqrt (1 + 6.928)= 7 дм.,,, sqrt- это квадратный корень; 2- это квадрат. ; /_ - это угол.
(К примеру до точки С: )
DC = sqrt (AD2 + AC2) = sqrt (1 + 8) = 8,06225 дм.