Сделай себе рисунок, чтобы было понятно
По свойству равнобедренных треугольников, высота, проведенная к основанию, является как высотой, так и медианой для AC, т. е. AD=DC
Рассмотрим треугольник ABD (угол ADB - прямой)
Найдем по теореме Пифагора сторону AD
AD² = AB² - BD² = 10² - 6² = 100 - 36 = 64
AD = √64 = 8 (см)
AC = 8 + 8 = 16 (см)
Рассмотрим треугольник ABC
Найдем площадь по формуле Герона
S = √(p(p-a)(p-b)(p-c))
p = (10 + 10 + 16) / 2 = 18 (см)
S = √(18 * 8 * 8 * 2) = √(9 * 2 * 8 * 8 * 2) = 3 * 2 * 8 = 48 (см²)
R = abc / 4S
R = 10 * 10 * 16 / 4 * 48 =
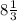 (см)
(см)
Сделай лучшим )
На сторонах угла∡ABC точки A и C находятся в равных расстояниях от вершины угла BA=BC. Через эти точки к сторонам угла проведены перпендикуляры AE⊥BA CD⊥BC.
1. Чтобы доказать равенство ΔAFD и ΔCFE, докажем, что ΔBAE и ΔBCD, по второму признаку равенства треугольников:
BA=BC
∡BAF=∡BCF=90°
∡ABC — общий.
В этих треугольниках равны все соответсвующие эелементы, в том числе BD=BE, ∡D=∡E.
Если BD=BE и BA=BC, то BD−BA=BE−BC, то есть AD=CE.
Очевидно равенство ΔAFD и ΔCFE также доказываем по второму признаку равенства треугольников:
AD=CE
∡DAF=∡ECF=90°
∡D=∡
Подробнее - на -
Объяснение: