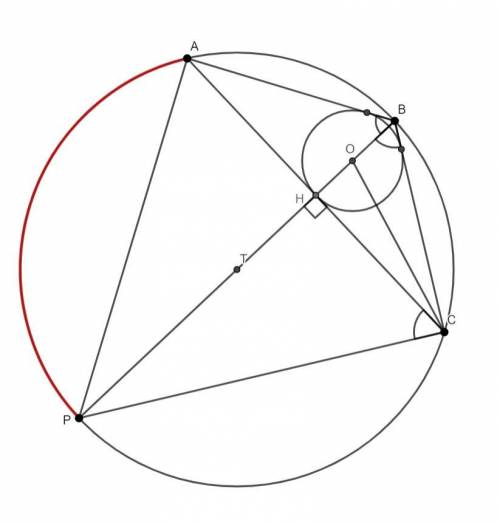
а)
Центр вписанной окружности лежит на пересечении биссектрис. Откуда CO - биссектриса ∠ACB; BO - биссектриса ∠ABC. Биссектриса делит угол пополам.
В ΔOBC: ∠POC - внешний, поэтому равен сумме двух внутренних углов треугольника не смежных с ним. ∠POC = ∠OBC+∠BCO.
∠PCA = ∠PBA, как вписанные углы опирающиеся на одну дугу AP.
∠PBA = ∠PBC, как углы при биссектрисе. Так же ∠ACO = ∠BCO.
В ΔPOC:
∠PCO = ∠PCA+∠ACO = ∠PBC+∠BCO;
∠POC = ∠OBC+∠BCO;
∠PCO = ∠POC ⇒ ΔPOC - равнобедренный (OC - основание) значит, PO=PC, что и требовалось доказать.
б)
Пусть PH⊥AC и H∈AC, тогда PH=21. ∠ABC=120°. T - центр описанной окружности около ΔABC.
Четырёхугольник PABC - вписан в окружность, поэтому ∠APC+∠ABC=180°;
∠APC = 180°-120° = 60°.
∠PCA = ∠PBA = ∠ABC:2 = 120°:2 = 60°
В ΔPCA: ∠PCA=60°; ∠APC =60°; ΔPCA - равнобедренный, с углом при основании в 60°, поэтому это равносторонний треугольник.
Радиус описанной около ΔABC равен радиусу описанной около ΔPCA т.к. это одна окружность.
PH - высота правильного ΔPCA, а значит и медиана.
Центр описанной окружности около правильного треугольника является центром треугольника, в том числе и центром тяжести (т. пересечения медиан). Поэтому радиус описанной равен 2/3 от высоты.
PT =  PH = 21·2/3 = 14
PH = 21·2/3 = 14
ответ: 14.
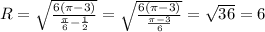
Дано : a║b; a║β
Доказать : b║β или b⊂β
Построим прямую c║a, которая лежит в плоскости β. По свойству параллельных прямых :
b║a и c║a ⇒ b║c ⇒ b║β или b⊂β
Прямая параллельна плоскости либо лежит в плоскости, так как параллельна прямой, лежащей в этой плоскости.