Объяснение:
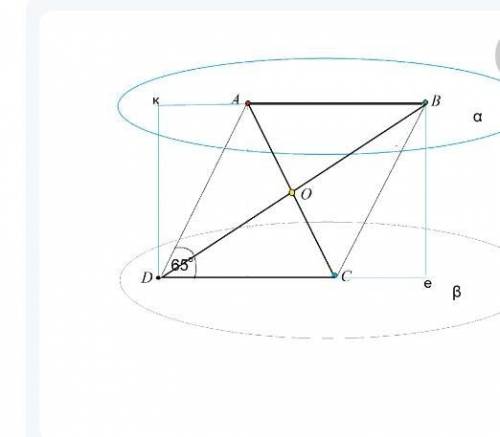
Точки А и В лежат в плоскости альфа, а точки С и D- в плоскости бета, причём альфа параллельна бета, АВ=СД, а отрезки АС и ВD пересекаются.
а) докажите, что АВ параллельна СD.
б) Один из углов четырёхугольника АВСD равен 65 градусов. Найдите остальные углы
а) АС и ВD пересекаются.
Через две пересекающиеся прямые можно провести плоскость, и притом только одну; то же справедливо и для параллельных прямых.
Следовательно, прямые АВ и СD лежат в той же плоскости. что АС и ВD.
Проведем из D и В перпендикуляры кD и Ве к противоположной плоскости.
Т.к. плоскости α и β параллельны, то кD и Ве параллельны и равны ( на основании того, что это - перпендикуляры между параллельными плоскостями)
Прямые кВ и Dе лежат в одной плоскости кВeD, расстояние между ними равно, следовательно, они параллельны.
АВ принадлежит кВ, DС принадлежит Де, следовательно, АВ||СD.
б) Четырехугольник, в котором противоположные стороны равны и параллельны, - параллелограмм.
Противоположные углы параллелограмма равны.
Сумма углов, прилежащих к одной стороне параллелограмма, равна 180°
Острые углы четырехугольника АВСD равны по 65°. Тупые по-180-65=115°———
Даны вершины пирамиды АВСD А(1,2,3), В(2;0;0), С(3;2;5), D(4;0;0).
1) Находим векторы АВ и АС.
АВ = (2-1; 0-2; 0-3) = (1; -2; -3).
АС = (3-1; 2-2; 5-3) = (2; 0; 2).
Векторное произведение равно:
i j k| i j
1 -2 -3| 1 -2
2 0 2| 2 0 = -4i - 6j + 0k - 2j - 0i + 4k = 4i - 8j + 4k = (4; -8; 4).
S = (1/2)*√(16 + 64 + 16) = (1/2)*√96 = 2√6 ≈ 4,898979.
2) Находим вектор АД = (3; -2; -3).
Смешанное произведение (АВ*АС)хАД равно:
4 -8 4
3 -2 -3 = 12 + 16 - 12 = 16.
V = (1/6)*16 = 8/3.