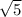раз (есть соответствующая формула)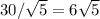
сторона ромба равна 16√3/4=4√3/см/,диагональ получаются равные сторонам, значит, половина диагонали равна 2√3, а половина второй диагонали найдется по теореме Пифагора, т.е.
√(16*3-4*3)=6/см/, тогда вторая диагональ равна 12 см, и площадь ромба, с одной стороны, равна половине произведения , т.е. диагоналей 12*4√3/2=24√3/см²/, а, впрочем, можно было еще проще, (4√3)²*sin60°=16*3*√3/2=24√3/cм²/, и эта же площадь равна произведению стороны на высоту, которая равна двум радиусам, значит, 24√3/(4√3*2)=3/см/- радиус вписанной окружности.
Второй признак равенства треугольников - если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.
Объяснение:
в равнобедренном треугольнике медиана является биссектрисой и высотой
Сторона ВМ общая для обоих треугольников.
Угол PBM=MBK
Угол BMP=BMK
Второй признак равенства треугольников - если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.
Докажем, что меньший треугольник также равносторонний. Так как он отсекается прямой, параллельной стороне исходного треугольника, два угла маленького треугольника, прилежащие к этой прямой, соответственно равны двум углам исходного треугольника и равны 60 градусам, а третий угол совпадает с углом исходного треугольника, так что тоже равен 60 градусам, что и требовалось.
Теперь мы опять можем воспользоваться формулой площади равностороннего треугольника. Пусть сторона меньшего треугольника равна b, тогда его площадь будет равна √3b²/4. Значит, √3b²/4=5√3, откуда b²=20, b=2√5. Периметр равностороннего треугольника равен его утроенной стороне, то есть P=3b=6√5
ответ: 6√5