Объяснение:
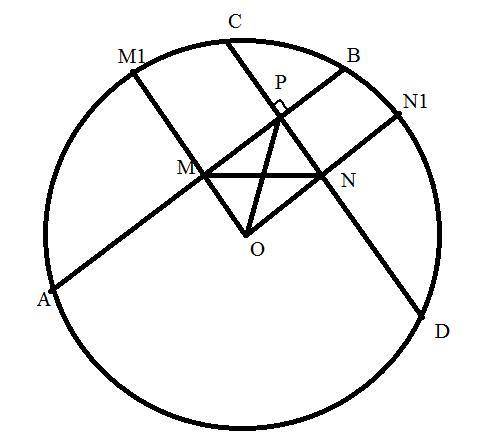
Пусть АВ и CD - хорды, перпендикулярные друг к другу, пересекающиеся в точке Р. Точки M и N - середины хорд АВ и CD.
Проведём радиусы ОМ1 и ОN1 через эти точки M и N. Эти радиусы будут перпендикулярны хордам АВ и CD соответственно по свойству хорды и радиуса (ну или доказывается через равнобедренный треугольник с боковыми сторонами, равными радиусу и медианой, проведённой к основанию - она же будет высотой).
Значит <OMP=<ONP=90°, при этом <MPN=90° по условию. Значит в четырёхугольнике OMPN оставшийся 4й угол <MON также равен 90° => OMPN - прямоугольник. В прямоугольнике диагонали равны, значит OP=MN, чтд.
значит МК=14/2=7
МК и АС параллельны друг другу, из этого <BAC=72 значит соответственный к нему угол ВМК так же равен 72 градусам
ответ: МК=7см; ВМК=72