Сумма смежных углов равна 180°
∠В и внешний ∠ при вершине В - смежные.
=> ∠В = 180° - 120° = 60°
∠А = ∠С, по свойству равнобедренного треугольника.
180° - 60° = 120° - сумма ∠А и ∠С
∠А = ∠С = 120°/2 = 60°.
Вывод:
этот треугольник - равносторонний (∠А = ∠В = ∠С = 60°)
ответ: 60°, 60°, 60°.
Внешний угол треугольника равен сумме двух внутренних углов треугольника несмежных с ним.
=> ∠А + ∠С = 120°
∠А = ∠С, по свойству равнобедренного треугольника.
=> ∠А = ∠С = 120°/2 = 60°
Сумма углов треугольника равна 180°
=> ∠В = 180˚ - (60˚ + 60˚) = 60˚
Вывод:
этот треугольник - равносторонний (∠А = ∠В = ∠С = 60°)
ответ: 60°, 60°, 60°.
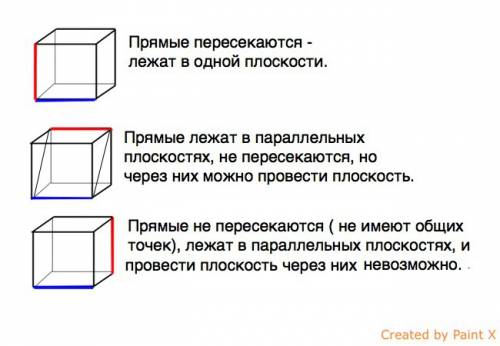
Поскольку в условии задачи не указано, лежат ли прямые в одной плоскости или нет, то они необязательно параллельны.
В планиметрии две прямые могут быть параллельными или пересекаться.
Две прямые в пространстве параллельны друг другу, пересекаются или скрещиваются.
Если две прямые лежат в одной плоскости и не пересекаются, то они - параллельны.
. В стереометрии две прямые могут не пересекаться, но в то же время не быть параллельными.
Прямые, которые не имеют общих точек и не параллельны, называются скрещивающимися.
Скрещивающиеся прямые лежат в параллельных плоскостях, но плоскость провести через них, как это можно сделать через две параллельные прямые, невозможно
Рассмотрим это на ребрах куба (см. приложение)
tg45 = 1
1/2 + 1 = 1/2 + 2/2 = 3/2 = 1,5