8см
Объяснение:
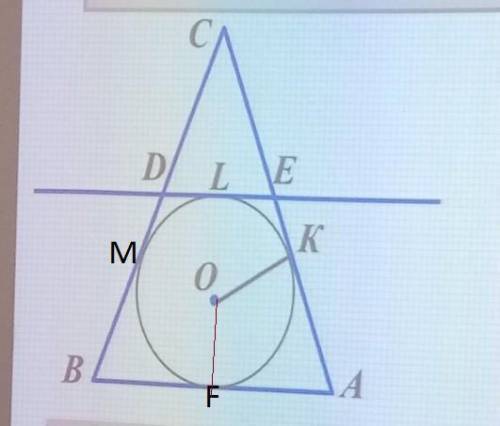
Теорема: Отрезки касательных к окружности, проведенные из одной точки, равны:
1) BM = BF MD = DL
FA = KA EK = LE
2) Pcde = CD + DE + CE =
= CD + (DL + LE) + CE = (CD + MD) + (EK +CE) = CM + CK =
= (BC - BM) + (AC - AK)
Т.к. ΔАВС - равнобедренный, то
ВС = АС = (Pabc - AB)/2 = (20 - 6)/2 = 7(cм)
Pcde = ВС + АС - ВМ - АК = 2 * 7 - ВМ - АК = 14 - ВМ - АК
3) Центр вписанной окружности лежит на биссектрисе. Но в равнобедренном треугольнике высота, а так же медиана и биссектриса, проведенные к основанию совпадают, следовательно, СF - медиана и делит АВ пополам:
ВF = FA = 6 / 2 = 3 (см)
4) Т.к. отрезки касательных к окружности, проведенные из одной точки, равны, то
BF = BM = 3(см)
FA = AK = 3(см)
Pcde = 14- ВМ - АК = 14 -2*3 = 8(см)
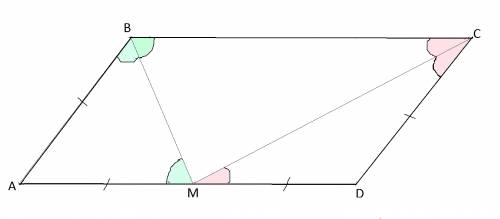
Сделаем рисунок к задаче.
Обозначим вершины параллеограмма привычными буквами АВСD.
Проведем биссектрисы углов В и С, которые пересекутся на АD в точке М.
Биссектрисы образовали со сторонами параллелограмма треугольники, причем
∠ СВМ= ∠ АМВ по свойству углов при пересечении параллельных прямых и секущей, а
∠ АВМ= ∠МВС - как половины угла В.
То же самое с углами ВСМ и СМD.
Раз углы при основании ВМ Δ АВМ и основании СМ Δ СМD равны,
оба этих треугольника - равнобедренные.
В треугольнике АВМ сторона АВ равна стороне АМ,
В треугольнике МDС сторона МD равна стороне СD.
Но АВСD- параллелограмм, и стороны АВ и CD равны по определению.
Следовательно, АМ=MD и АD=2АВ ( или 2 CD, что одно и то же)
Р АВСD= 2( АВ+АD) Подставим в значение периметра 2 АВ вместо AD.
Р АВСD= 2( АВ+2АВ)
30= 6 АВ
АВ=5 см
Ответ: Длина короткой стороны параллелограмма равна 5 см
Вектор это просто стрелка из одной точки в другую. Длина вектора - длина отрезка между такими точками.
А координаты вектора - это точка, в кторую укажет стрелка, если мы ее нарисуем из начала координат.
Собственно, если вектор перенести в любое другое место, то его длина от этого не изменится, но длину легче считать, когда он отложен от начала координат.
Найдем координаты. Перенесем точку А в точку (0,0). Для этого надо вторую координату точки А увеличить на 3.
Теперь перенесем точку Б. Здесь надо просто повторить то, что сделали для точки А, то есть увеличить вторую координату на 3.
После перемещения имеем вектор из точки (0,0) в точку (-1,3). Точка (-1,3) - и есть координаты вектора АВ.
Длина вектора АВ собвпадает с длиной вектора из (0,0) в (-1,3), потому что это один и тот же вектор, просто передвинут в другое место.
Потому считаем длину вектора из точки (0,0) в (-1,3). Это делается по теореме Пифагора
Итого:
координаты - (-1, 3)
длина -