№10
а)Т.к. ∠Д=∠В=90°, то треугольники прямоугольные. В них АД=СВ- по условию,
ДВ-общая. Значит, треугольники АДВ и СВД равны по двум катетам.
№6 ΔСЕД=ΔСFД, ∠Е=∠F=90град.
СД -общая. ЕД=FД по условию, треуг. равны по катету и гипотенузе.
б) ΔАЕД=ΔВFД т.к. ∠АЕД=∠ДFВ = 90°, АД=ВД по условию,
ЕД=FД по условию. треуг. равны по гипотенузе и катету.
в) треугольники АСД И ВСД равны, т.к. составлены из двух равных, а именно АСД из треугольников АЕД И СЕД, треугольник ВСД составлен из треугольников ВFД и ДFС
№7.
а)ΔМSR=ΔNRS, в них ∠M=∠N=90°, ∠NRS=∠MSR по условию, RS-общая. Треугольники равны по острому углу и гипотенузе.
б) Если от равных треугольников NRS и MSR отнять один и тот же ΔRTS, то останутся равные треугольники, а именно
ΔRMT=ΔSNT
№8.
а)∠К=∠L=90°
ΔМLN =ΔNКМ. В них МN-общая, ∠М=∠N по условию, значит треугольники равны по острому углу и гипотенузе.
б)ΔКRМ=Δ LRN, (∠L=∠ К=90°) т.к. если от равных ΔМLN и ΔNКМ отнять один и тот же треугольник МRN, то останутся тоже равные треугольники.
№9. ΔАДЕ=ΔВFМ, в них ∠М=∠Е=90°, АД=FВ по условию,
и так как ДС=FC, то АС=СВ, и ΔАСВ- равнобедренный, в нем углы при основании равны. угол А равен углу В. Значит, треугольники равны по острому углу и гипотенузе.
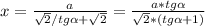
...............................Решение на фото внизу