Объяснение:
1. Если внутренние накрест лежащие углы равны, то прямые параллельны.
∠70°=∠70° ⇒
a║b
2. Если сумма внутренних односторонних углов равна 180, то то прямые параллельны.
∠110+∠70=180°⇒
c║d
3. Если соответственные углы равны, то прямые параллельны.
∠a=∠a
MD║|NK
4. Если соответственные углы равны, то прямые параллельны.
∠90=∠90
m║n
5. Если внутренние накрест лежащие углы равны, то прямые параллельны.
BC║AD
AB║CD
6. Если внутренние накрест лежащие углы равны, то прямые параллельны
∠EFL=∠FLK ⇒ EF║LK
∠EKF=∠KEL⇒ FK║EL
7. Если внутренние накрест лежащие углы равны, то прямые параллельны
∠NPM=∠PMQ ⇒NP║MQ
∠NMP=∠MPQ⇒NM║PQ
8. ΔAOB=ΔCOD (по двум сторонам и углу между ними)⇒
∠BAO=∠ODC если внутренние накрест лежащие углы равны, то прямые параллельны
AB║CD
9. ΔOXY=ΔOYZ по трем сторонам ⇒
∠XYO=∠YOZ ⇒ XY║OZ
∠XOY=∠OYZ⇒ OX║YZ
10.
UR║ST (внутренние накрест лежащие углы равны)
ΔRUO=ΔOST (по стороне и двум прилежащим к ней углам) ⇒
∠TRU=∠STR ⇒ RS║UT
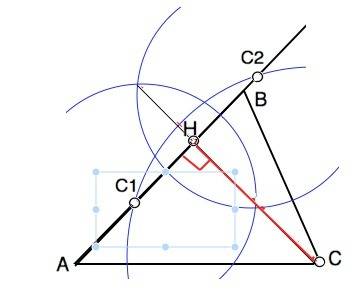
Для построения высоты применяется метод построения перпендикуляра из точки к прямой.
Построениевысоты из вершины С.
Из С, как из центра, чертим полуокружность и делаем насечки на прямой АВ в точках С1 и С2. Стороны СС1 и СС2 треугольника С1СС2 - радиусы, поэтому он равнобедренный.
Из точек С1 и С2 как из центров, строим полуокружности равного радиуса так, чтобы они пересеклись по обе стороны от АВ.
Через точки их пересечения к вершине С проводим отрезок НС. Отрезки С1Н=НС2, а СН - перпендикуляр к АВ.
Высоты из А и В строятся точно так же.