Объяснение:
10)
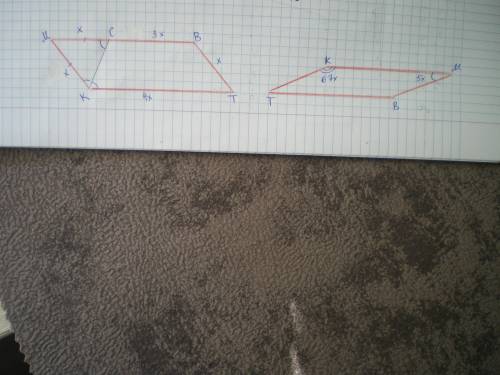
Дано: КМВТ - параллелограмм, Р=65 см, КС - биссектриса, МС/ВС=1/3.
Найти МВ.
∠МКС=∠СКТ по определению биссектрисы
∠СКТ=∠МСК как внутренние накрест лежащие при МВ║КТ и секущей КС
значит, ΔМКС - равнобедренный и МК=МС.
Пусть МС=МК=ВТ=х см, тогда ВС=3х см, КТ=МВ=х+3х=4х см.
Составим уравнение: х+х+4х+4х=65
10х=65; х=6,5
МВ=КТ=6,5 * 4 = 26 см.
ответ: 26 см.
11)
Дано: КМВТ - параллелограмм ∠М/∠К=5/67. Найти ∠К.
Сумма углов параллелограмма, прилегающих к одной стороне, составляет 180°.
Пусть ∠5х°, тогда ∠К=67х°.
Составим уравнение:
5х+67х=180; 72х=180; х=2,5
∠К=67*2,5=167,5°
ответ: 167,5°
Площадь трапеции находится по формуле
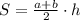
где a, b -- основания трапеции, h -- высота.
h = 10 см, S = 240 см² по условию
Пусть меньшее основание равно x см, тогда большее равно (x + 4) см.
Составим уравнение, используя формулу площади трапеции:
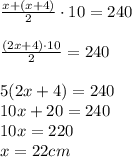
Таким образом, меньшее основание BC равно 22 см, а большее AD равно (22+4) = 26 см.
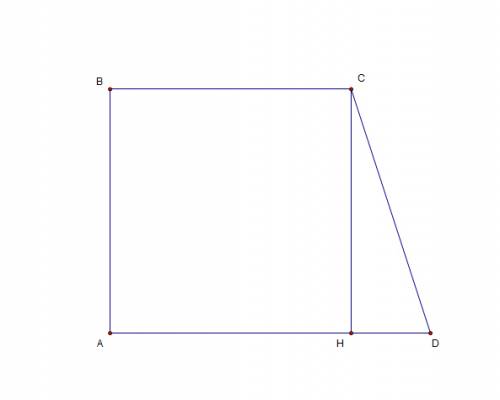
В прямоугольной трапеции одна из боковых сторон равна высоте, то есть AB = 10 см.
Проведём из точки С высоту CH. Тогда HD = AD - BC = 26 - 22 = 4 см
CH = h = 10 см. По теореме Пифагора найдём CD:
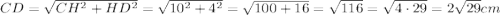
ответ: 10 см, 22 см, 26 см, 2√29 см
АС=ВС ⇒ ∆ АВС равнобедренный.
Внешний угол при вершине С=60° и по свойтву внешнего угла равен сумме двух внутренних, не смежных с ним.
Т.к. ∆ АСВ равнобедренный, ∠А=∠С=60°:2=30°.
Угол АСВ=180°-60°=120° (как смежный)
По т.синусов
АВ:sin120°=AC:sin30°
АВ:(√3/2)=6√3:(1/2)–
AB=6√3•√3=18 см