Дается один из возможных вариантов решения. ( На сайте есть и другой).
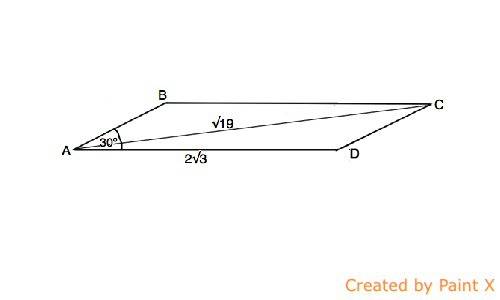
Пусть параллелограмм будет АВСD,
сторона АD=2√3, диагональ АС=√19, ∠ ВАD=30°
Сумма углов параллелограмма, прилежащих к одной стороне, равна 180° ( из свойства углов при параллельных прямых и секущей).
Тогда ∠ АDС=150°
По т.косинусов из ∆ АDС:
АС²=АD² +СD² - 2•AD•CD•cos ∠ADC
Примем СД=х
cos150ª= -cos30º= -(√3):2
19=12+х²-2•2√3•(-√3):2 ⇒
х²+6х-7=0⇒
D=b²-4ac=6²-4•-7=64
x₁=-(6)+√64):2=1;
х₂= -(6)-√64):2=-7 ( не подходит)
Противоположные стороны параллелограмма равны. АВ=CD
Меньшая сторона параллелограмма равна 1 см.
Расстояние между прямым В и С будет зависеть от расположения прямой С которая может находиться по разные стороны от прямой А на расстоянии 6дм тогда, при условии что расстояние от А до В равно 4дм,
расстояние между В и С можт быть
1) 6-4=2 Дм при условии что В и С лежат по одну сторону от А
2) 6+4=10 Дм при условии что В и С лежат по разные стороны от А