Sabcd = 150 см².
Объяснение:
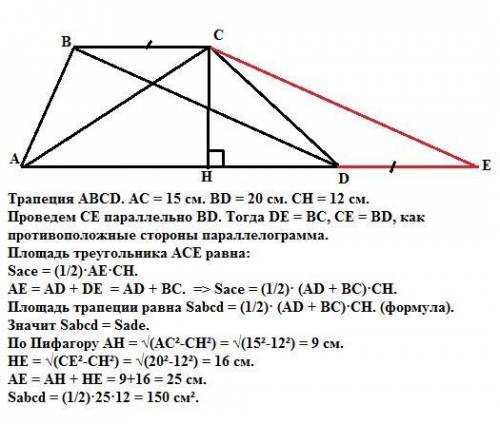
Трапеция АВСD. АС =15 см. ВD = 20 см. СН =12 см.
Проведем СЕ параллельно ВD. Тогда DЕ = ВС, СЕ = ВD, как противоположные стороны параллелограмма.
Площадь треугольника АСЕ равна:
Sace = (1/2)·АЕ·СН.
АE = АD + DЕ = АD + ВС. =>
Sace = (1/2)·(АD + ВС)·СН.
Площадь трапеции равна
Sabcd = (1/2)·(АD + ВС)·СН. (формула).
Значит Sabcd = Sade.
По Пифагору АН = √(АС²-СН²) = √(15²-12²) = 9 см.
НЕ = √(СЕ²-СН²) = √(20²-12²) =16 см.
АЕ = АH + HЕ = 9+16 =25 см.
Sabcd = (1/2)·25·12 = 150 см².
Точка М образует с основаниями трапеции два подобных треугольника (равные углы). Пусть искомое расстояние х, тогда из подобия треугольников составим пропорцию х/1.6=(х+4.4)/4.8 решая данное уравнение получаем 4.8х=1.6х+1.6*4.4⇒ 3.2х=7.04⇒ х=2.2
ответ:2.2см
Подробнее - на -