Question

Решить . 1. из точки к плоскости проведён перпендикуляр и наклонную. длина проекции наклонной равна 6 см. найдите длину перпендикуляра, если угол между перпендикуляром и наклонной равен 30 градусов. 2. площадь прямоугольника равна 192 см, а периметр - 56 см. точка размещена от его плоскости на расстоянии 24 см. найдите расстояние от данной точки до вершин прямоугольника, если эти расстояния равны между собой. 3. прямая fb перпендикулярна плоскости треугольника авс. точка f равноудалена от точек а и с. найдите длину отрезка fb, если ас=6см, сва=120 градусов, сfа=90 градусов.

Answer 1

1.
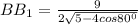
ΔАВС: ∠АВС = 90°, ∠ВАС = 30°,
             tg30° = BC / AB
            1/√3 = 6 / AB
             AB = 6√3 см

2.
Sabcd = ab = 192
Pabcd = 2(a + b) = 56

Получаем систему уравнений:
ab = 192
a + b = 28

b = 28 - a
28a - a² = 192              решим второе

a² - 28a + 192 = 0
D/4 = 14² - 192 = 196 - 192 = 4
a = 14 + 2 = 16            или              a = 14 - 2 = 12
b = 12                                                b = 16

Итак, стороны прямоугольника 12 см и 16 см.
МО - перпендикуляр к плоскости прямоугольника.
Наклонные, проведенные из точки М, равны, значит равны и их проекции, т.е. АО = ОВ = ОС = OD, ⇒ О - точка пересечения диагоналей.
ΔАВС: ∠АВС = 90°, по теореме Пифагора
             АС = √(АВ² + ВС²) = √(256 + 144) = √400 = 20 см
ОА = 10 см

ΔМОА: ∠МОА = 90°, по теореме Пифагора
               МА = √(МО² + ОА²) = √(576 + 100) = √676 = 26 см

3.
Наклонные FA и FC равны, значит равны и их проекции:
ВА = ВС = х.
Из треугольника АВС по теореме косинусов:
АС² = АВ² + ВС² - 2·АВ·ВС·cos120°
36 = x² + x² - 2·x·x·(- 0,5)
36 = 2x² + x²
36 = 3x²
x² = 12
x = 2√3 cм

Из ΔAFC по теореме Пифагора
а² + а² = АС²
2а² = 36
a² = 18
a = 3√2 см

Из ΔABF по теореме Пифагора
FB = √(FA² - AB²) = √(18 - 12) = √6 см