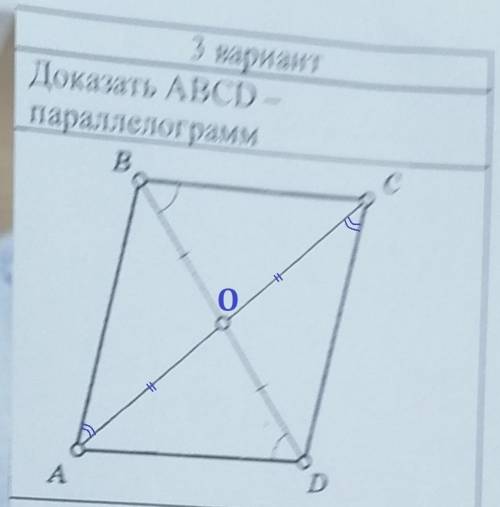
Параллелограмм - это четырехугольник, у которого противолежащие стороны попарно параллельны.
Если мы докажем, что BC║AD и AB║CD, то докажем, что ABCD параллелограмм.
1) ∠DBC = ∠BDA по условию, а это внутренние накрест лежащие углы при прямых BC и AD и секущей BD ⇒ BC║AD. (если внутренние накрест лежащие угли при двух прямых и секущей равны, то эти прямые параллельны).
2) ΔBOC = ΔAOD по второму признаку (стороне и двум углам):
BO = OD по условию, ∠OBC = ∠ODA по условию, ∠BOC = ∠AOD вертикальные углы.
В равных треугольниках соответствующие стороны равны. AO = OC
3) ΔAOB = ΔCOD по первому признаку:
BO = OD по условию, AO = OC по доказанному, ∠AOB = ∠COD - вертикальные углы.
Из равенства треугольников следует равенство соответствующих углов.
∠BAO = ∠DCO, это внутренние накрест лежащие углы при прямых AB и CD и секущей AC. ⇒ AB ║CD
4) В четырехугольнике ABCD AD║BC и AB ║ CD. Четырехугольник ABCD параллелограмм.
Доказано.
Дана правильная четырехугольная пирамида SАВСД, длина бокового ребра которой равна L = 3 см, а стороны основания a = 2√3 см.
Проведём осевое сечение через 2 боковых ребра.
В сечении равнобедренный треугольник АSС с боковыми сторонами L = 3 см и основанием - диагональ квадрата основания d = a√2 = (2√3)*√3 = 2√6 см.
Высота Н пирамиды равна:
Н = √(L² - (d/2)²) = √(9 - 6) = √3 см.
Перпендикуляр из центра основания пирамиды на боковое ребро (пусть это ОК) - это высота треугольника ОSС, она равна (√3*√6)/3 = √2 см.
Искомый угол лежит в перпендикулярном сечении к боковому ребру.
В сечении - треугольник ВКД.
Апофема А = √(3² - (2√3/2)²) = √(9 - 6) = √3 см.
КД - высота, она равна 2S/L = (2*((1/2)*2√3*√6))/3 = 2√2 см.
То есть она как гипотенуза треугольника ОКД в 2 раза больше катета ОК, а угол КДО равен 30 градусов.
Отсюда искомый угол ВКД равен 2*60 = 120 градусов.