1. Осевое сечение цилиндра - квадрат ⇒ диаметр основания равен высоте конуса, т.е. стороне этого квадрата. Диагональ делит квадрат на два равных прямоугольных с острыми углами 45°. Сторона квадрата (диаметр основания) равен 36•sin45°=36•1/√2=18√2 см. R=d:2=9√2 см .
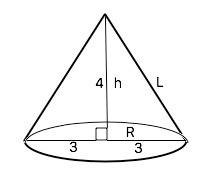
2. Высота и радиус конуса – катеты прямоугольного (египетского) треугольника, его образующая – гипотенуза . R=d:2=3 м. ⇒ По т.Пифагора образующая L=√(4²+3²)=5 м. Осевое сечение конуса - равнобедренный треугольник. Ѕ(осев)=h•R=4•3=12м²
Ѕ(полн)=Ѕ(осн)+Ѕ(бок)
Ѕ(полн)=πR²+πRL=π3²+π•3•5=24π м²
Объяснение:
3. 1) Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания,
значит ∠ ОКМ=90°-7°=83° .
2) ∆ ОКМ- равнобедренный (ОК=КМ=r) , значит ∠ОКМ=∠ОМK=83°.
4. 1) Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания,
значит ∠ ОКМ=90°-84°=6°
2) ∆ ОКМ- равнобедренный (ОК=КМ=r) , значит ∠ОКМ=∠ОМK=6°.
5. ∠ ABC =90°(вписанный), т.к ∪ АС=180° (опирается на диаметр АС). Тогда ∠С=180°-90°-75°=25°
6. 1) ∪ AN=73°·2=146° (стягивает вписанный ∠ NBA). Тогда
∪ NB =∪ AB-∪AN=180°-146°=34°.
2) ∠NMB=34°/2=17° (вписанный не центральный угол)
7. 1) ∆ АОВ- равнобедренный(АО=ОВ=r), значит ∠ОАВ=∠АВО=15°. Тогда ∠ОВС =56°-15°=41°.
2) ∆ ВОС- равнобедренный(ВО=ОС=r), значит ∠ОВС=∠ВСО=41°.
8. ∆ АОВ =∆ СОD (AO=OD=r, CO=OB=r, ∠AОВ =∠CОD-вертикальные ), значит ∠ОАВ =∠ОСD=25°
...
cosA=sinB=0,5
sinB=CH/BC=>CH=BC*sinB
CH=8*0.5=4