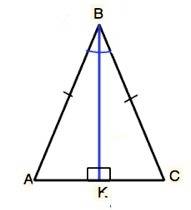
В ∆ АВС стороны АВ=ВС, ВК - биссектриса.
Рассмотрим ∆ АВК и ∆ СВК.
АВ=ВС, ВК - общая, угол АВК=СВК. ⇒ Треугольники равны по первому признаку: по двум сторонам и углу, заключенному между ними.
Из равенства треугольников ∆ АВК и ∆ СВК следует МК=СК⇒
ВК - медиана ∆ АВС.
В равных треугольниках углы, противолежащие равным сторонам, равны. ⇒
∠ВКА=∠ВКС
АКС – развернутый угол и равен 180°.
ВК делит его на два равных с градусной мерой 180°:2=90° ⇒
ВК⊥АС и является высотой равнобедренного треугольника АВС.
15.
Угол MSK смежен с углом KSN, значит угол KSN равен 180° - 108° = 72°, так как сумма смежных углов равна 180°
Угол NKM равен 180° - 90° - 72° = 22°, так как сумма углов треугольника равна 180°.
Угол KNM = 90°, это видно из рисунка, он обозначен как прямой угол
16.
Числовых данных нет, поэтому буду решать в общем виде.
Угол ABC равен 30°, так как он смежен с углом 150°, а сумма смежных углов равна 180°
Угол CAB равен 60°, так как сумма углов треугольника равна 180° а два других угла равны 30° и 90°. 180° - 90° - 30° = 60°
Углы CAD и DAB равны по 30°, так как AD биссектриса, а биссектриса делит угол пополам. CD - катет, лежащий против угла в 30°, значит он равен половине гипотенузы. CD = 0,5AD
Так как углы DAB и DBA равны, то треугольник BDA - равнобедренный и AD = DB
Отсюда CB = CD+DB = 0,5AD + DB, а так как AD = DB, то CB = 0,5AD+AD=1,5AD
17.
Обратная задача задаче 16. Так как PS = 0,5 RS, то угол PRS равен 30°, значит угол PRQ = 60°, так как RS - биссектриса.
Угол RQP равен 30°(смотрите задачу 16). Значит угол RQT равно 180° - 30° = 150°
SQ = 15,6, так как треугольник RSQ - равнобедренный и RS = SQ(смотрите решение задачи номер 16)
18.
Периметр треугольника MKR равен MK + KR + MR = 32
Треугольники MRE и NRE равны по двум сторонам и углу между ними, так как RE = RE, ME = NE, угол MER равен углу NER и равен 90°
Значит MR = NR
KR + MR = KR + NR = KN = 26
Подставляем в формулу периметра:
P = MK + KR + MR = MK + KR + NR = MK + KN = 32
Значит MK = 32 - KN = 32 - 26 = 6
MK = 6