ΔАВС - равносторонний, по условию С₁О - это отрезок, соединяющий центр О основания АВС с вершиной С₁, и перпендикулрный плоскости основания АВС, значит, пирамида C₁ABC - правильная, но не только, это и правильный тетраэдр, пусть все его стороны равны 1, тогда можно заметить, что в пирамиде С₁АВВ₁А₁ в основании лежит ромб, а её высота падает в точку Н - точку пересечения диагоналей ромба, но её боковые грани состоят из правильных треугольников, а значит, что и их прокеции будут равны и ВАУ! мы получаем в основании квадрат! То есть сама изначальная призма состоит из правильного тетраэдра и правильной четырёхугольной пирамиды, все стороны которых равны по 1.
∠(АА₁;(АВС₁)) = ∠(ВВ₁;(АВС₁))
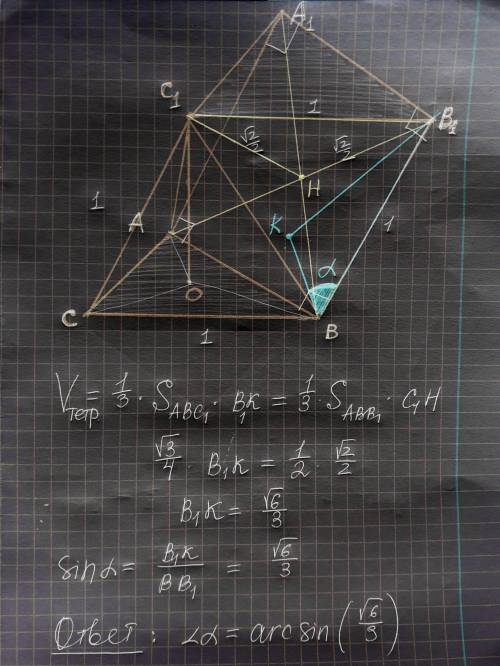
Рассмотрим пирамиду В₁АВС₁ и возпользуемся методом площадей:
C₁H² + B₁H² = B₁C₁² ⇒ C₁H = √2/2 ; S (abc) = √3/2 ; S (abb₁) = 1/2
См. приложение. ответ: arcsin(√6/3)
0
Объяснение:
исходя из написанного (я догадываюсь) что a2 это а в квадрате , на будущее записывается это так a^2
исходя из теоремы пифагора для прямоугольного треугольника a^2+b^2=c^2 , но в условии не указано какие буквы за какую сторону отвечают(возможно это подвох ) , проверим .
Допустим A(которая a маленькая) у нас будет гипотенузой , тогда составим систему уравнений
a^2=b^2+c^2
a^2+b^2=5*c^2
тогда система уравнений имеет бесконечное множество решений, следовательно в условии задачи подразумевается что a и b это катеты , c это гипотенуза, тогда исходя из теоремы пифагора такого треугольника не существует