1
Избавься от ограничений
ПОПРОБУЙ ЗНАНИЯ ПЛЮС СЕГОДНЯ
angelikaliaka
08.12.2014
Геометрия
10 - 11 классы
+18 б.
ответ дан
сторона основания правильной четырехугольной пирамиды равна 6 см, высота - 4 см. Найти площадь полной поверхности.
1
СМОТРЕТЬ ОТВЕТ
Войди чтобы добавить комментарий
ответ, проверенный экспертом
4,0/5
7
Hrisula
главный мозг
7.5 тыс. ответов
16.7 млн пользователей, получивших
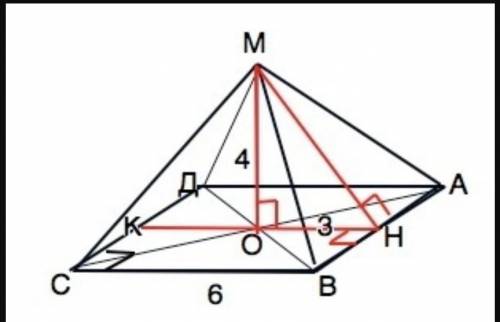
Обозначим пирамиду МАВСД.
Основание - квадрат со стороной 6 см. Высота МО=4 см.
МН- апофема ( высота боковой грани правильной пирамиды).
Площадь полной поверхности пирамиды - сумма площади основания и боковой поверхности.
S (бок)=0,5•Р•МН
Через основание высоты проведем КН║СВ.
КН⊥АВ. КН=ВС=6
ОН=КН:2=3
Из прямоугольного ∆ МОН по т.Пифагора
МН=5 см
S(бок)=0,5•4•6•5:2=60 см²
S(АВСД)=6²=36 см²
S(полн)=36+60=96 см²
Обозначим данные прямые через l0 и l, данные точки на прямой l0 - через A0, B0, C0, данные точки на прямой l - через A, B, C. Пусть l1 - произвольная прямая, не проходящая через точку A. Возьмем произвольную точку O0, не лежащую на прямых l0 и l1. Обозначим через P0 центральное проектирование прямой l0 на прямую l1 с центром в точке O0, а через A1, B1, C1 - проекции точек A0, B0, C0. Пусть l2 - произвольная прямая, проходящая через точку A, не совпадающая с прямой l и не проходящая через A1. Возьмем некоторую точку O1 на прямой AA1 и рассмотрим центральное проектирование P1 прямой l1 на l2 с центром в O1. Обозначим через A2, B2, C2 проекции точек A1, B1, C1. Ясно, что A2 совпадает с A. Наконец, пусть P2 - проектирование прямой l2 на прямую l, которое в том случае, когда прямые BB2 и CC2 не параллельны, является центральным проектированием с центром в точке пересечения этих прямых, а в том случае, когда прямые BB2 и CC2 параллельны, является параллельным проектированием вдоль одной из этих прямых. Композиция P2°P1°P0 является требуемым проективным преобразованием.
Объяснение:
пример
2) Якщо сторони 1 кута є доповняльними променями сторін другого. Вертикальні кути рівні.