Question

Ну ! даны две точки: а, лежащая на оси ординат и в (1; 0; 1).прямая ав составляет с плоскостью oxz угол 30 градусов. найти координаты точки а

Answer 1

Если сделать рисунок, то будет видно, что точка B лежит в пслокости OXZ, так как ордината точки B равна нулю. Рассмотрим треугольник ABO. Он прямоугольный, одна сторона его OA лежит на оси ординат. Из условия задачи угол ABO=30 градусов (это как раз угол пересечения прямой AB с осью OXZ). Найдем длину OA.

OA=OB*tgABO=OB*tg30

Чтобы найти OA, найдем чему равно OB.

Для этого опустим перпендикуляры из точки B на ось x (пересечение - точка K) и ось z (пересечение - точка L). Из координат точки B понятно, что BK=1, BL=1

Из теоремы Пифагора находим, что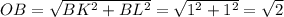 $OB=\sqrt{BK^2+BL^2}=\sqrt{1^2+1^2}=\sqrt{2}$

Теперь находим OA:

$OA=OB*tg30=\sqrt{2}*\frac{\sqrt{3}}{3}=\frac{\sqrt{6}}{3}$

OA - это и есть значение ординаты точки A

Так как A лежит на оси ординат, ее координаты x=0 и z=0

Возможны два случая:

1) A лежит в положительной части оси ординат

Тогда координаты точки будут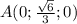 $A(0;\frac{\sqrt{6}}{3};0)$

2) A лежит в отрицательной части оси ординат

Тогда координаты точки будут $A(0;-\frac{\sqrt{6}}{3};0)$