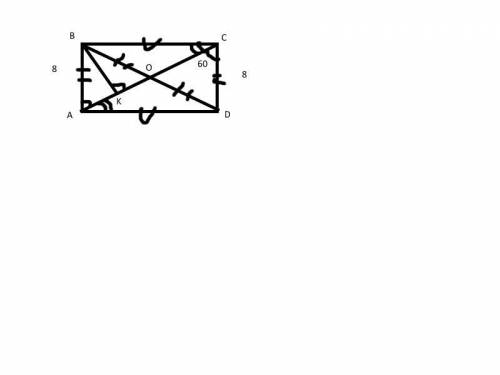
Дано: ABCD - прямоугольник
BK⊥AC
∠ACD=60°
AB=8 см
Найти: BD = ?
OK = ?
Т.к ABCD - прямоугольник, то AB=CD=8 см
∠OCD=∠BAO (н/л BC || AD и сек. AC) = 60°
∠BCO=∠OAD (н/л) = 90-60=30°
В прямоугольном ΔABC, ∠B=90°, ∠ACB=30°. Напротив угла в 30° в прямоугольном Δ лежит катет, равный половине гипотенузы => AB=0,5*AC => 8=0,5*AC => AC=8:0,5 => AC=16
Диагонали в прямоугольнике точкой пересечения делятся пополам => AO=OC=8 см.
ΔOCD - р/б т.к OC=CD => ∠COD=∠ODC. Сумма углов в треугольнике равна 180° => ∠COD=∠ODC= (180°-60°)/2=60° => ΔOCD - равносторонний по признаку => OD=OC=CD=8 см
BO=OD (диагональ делится пополам точкой пересечения)
BD=2*OD
BD=2*8
BD=16 см
ΔBOA - равносторонний (AB=BO=AO=8 см) => BK - высота, биссектриса и медиана => OK= 0,5*AO; OK=0,5*8; OK=4
ответ: BD = 16 см; OK = 4 см
Объяснение:
AH=120/2=60 (так как высота в равнобед. треуг. является и медианой)
BH= корень из 100^2-60^2=80 (по теореме Пифагора)
S= 1/2*120*80=480