В прямоугольном треугольнике высота, проведенная к гипотенузе, делит треугольник на подобные, а отрезки гипотенузы являются проекциями соседних катетов.
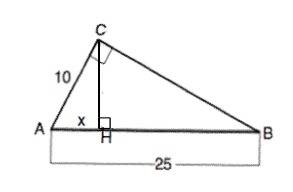
Пусть данный треугольник АВС с прямым углом С. Отрезок ВН - проекция катета ВС, которую нужно найти, а АН - проекция катета АС.
Каждый катет есть среднее пропорциональное между гипотенузой и проекцией катета на гипотенузу: =>
АС²=АВ•АН
100=25•АН=>
АН=4
ВН=25-4=21 (ед. длины)
----------
Можно сначала по т.Пифагора вычислить длину второго катета.
Затем из свойства катетов
ВН=ВС²:АВ получим ту же длину проекции.
Найти: S(ABCD)-?
Решение.1) ABCD-ромб==> <ABO=30 градусов (BO- бис., по свойству), OB=6 корней из 3
2) треугольник ABO- прямоугольный, tg ABO= AO/OB
AO=tg ABO*OBAO=(корень из 3 * 6 корней из 3)/3
AO=6
3) AO=OC (по свойству)AC=12
4) S(ABCD)=AC*BD/2
S(ABCD)=12*12 корней из 3/2
S(ABCD)=72 корня из 3