6 см
Объяснение:
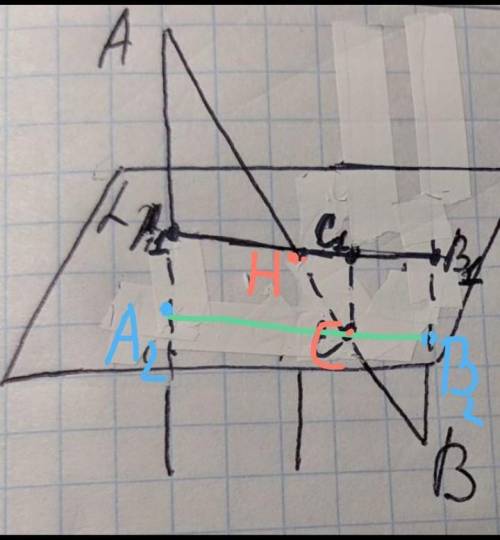
Точку пересечения АВ и А1В1 обозначим — Н (точка, в которой прямая АВ пересекает плоскость а)через точку С проведем прямую , параллельную прямой А1В1, которая соответственно пересечёт продолжение отрезка АА1 в точке А2, а отрезок ВВ1 в точке В2 (смотри прикреплённое изображение). Следовательно, А2В2 || А1В1.1) ∆ВВ1Н:
СВ2 || НВ1 (так как А2В2 || А1В1).СС1 и ВВ1 — перпендикуляры к В1Н. По условию СС1=4, ВВ1=10.Тогда В1В2=СС1=4 см, В2В=ВВ1-В2В1=10-4=6 см.
2) А1А2В2В1:
А2А1, СС1 и В2В1 — перпендикуляры к В1А1. А2В2 || А1В1.Тогда А2А1 = СС1 = В2В1 = 4 см.
3) ∆А2АС и ∆СВ2В:
<А1СВ = <В2СВ (как вертикальные углы),<АА2С=<ВВ2С=90° (так как А2А1, СС1 и В2В1 — перпендикуляры к В1А1, но А2В2 || А1В1. соответственно А2А1, СС1 и В2В1 — перпендикуляры к А2В2.)Тогда ∆ А2АС ~ ∆В2ВС,
отсюда следует, что
А2А/В2В = АС/ВС = А2С/В2С.
Из условия известно, что АС/ВС = 5/3.
тогда А2А / В2В = 5 / 3.
А2А = АА1 + А1А2 = АА1 + 4 (см).
В2В = 6 см.
(АА1+4) / 6 = 5 / 3 |×6
6*(АА1+4)/6 = 6*5/3
АА1+4 = 2*5=10
АА1=10-4=6 см
1) угол ТМР равен углу NTM - внутрение накрест лежащие угли при MP параллельно NK и секущей МТ, треугольник MNT равнобедренный MN=NT= 8
угол МРТ равен углу КТР - внутрение накрест лежащие угли при MP параллельно NK и секущей РТ, треугольник ТКР равнебедренный ТК=КР=8
NK=NT+TK=8+8=16
NK=MP=16 MN=KP=8
P=2MN+2NK=2*8+2*16=48
2) угол А=х, угол В=х+24
уг.А+уг.В+уг.С+уг.D=360
уг.А=уг.С уг.В=уг.D
2уг.А+2уг.В=360
2х+2(х+24)=360
2х+2х+48=360
4х=312
х=78
уг.А=уг.С=78 уг.В=уг.D=102