ответ: 75см; 10см; 20см; 12см; 18см; 24см
Объяснение:
3.
1) Находим сторону АС:
АС=АВ*2=17*2=34см
2) Находим сторону ВС:
ВС=АС-10=34=10=24см
3) Находим периметр треугольника АВС:
17+34+24=75см
4.
1) Находим сумму двух других сторон треугольника:
48-18=30см
Примем меньшую сторону за х, тогда большая сторона будет: х+10
2) Составим уравнение:
х+х+10=30
2х=20
х=10 см - это меньшая сторона
Большая сторона равна: 10+10=20см
5.
1) Примем стороны треугольника за 2, 3 и 4 части.
2) Находим из скольких частей состоит периметр треугольника:
2+3+4=9
3) Находим какая длина приходится на одну часть:
54/9=6см
4) Находим стороны треугольника:
6*2=12см
6*3=18см
6*4=24см
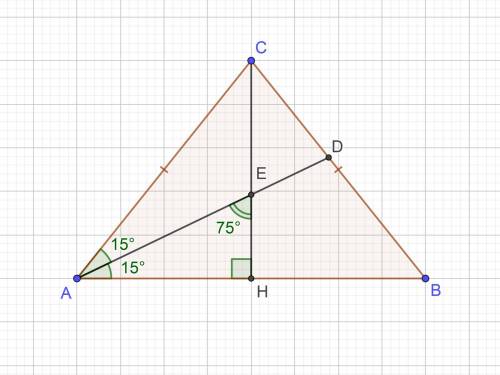
Дан равнобедренный ΔABC, AB — основание. ∠A = ∠B.
1-й случай: биссектриса угла при основании (AD), высота из вершины на основание тр-ка (CH). ∠AEH = 75°.
Так как CH — высота, тогда ΔAEH — прямоугольный, ∠AHE = 90° (EH ∈ CH)
∠EAH = 90°−∠AEH = 90°−75° = 15°
∠A = ∠EAH×2 = 15°×2 = 30°
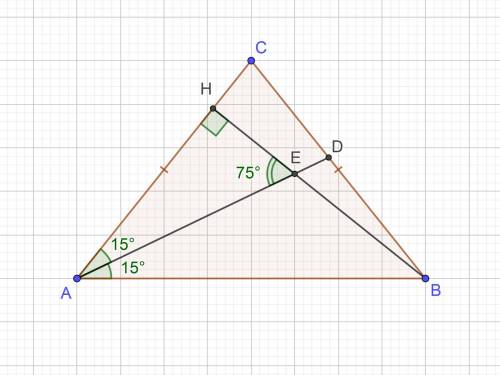
2-й случай: биссектриса угла при основании (AD), высота из противоположного угла при основании тр-ка (BH). ∠AEH = 75°.
Так как BH — высота, тогда ΔAEH — прямоугольный, ∠AHE = 90° (EH ∈ BH)
∠EAH = 90°−∠AEH = 90°−75° = 15°
∠A = ∠EAH×2 = 15°×2 = 30°
3-й случай: биссектриса угла при вершине (CD), высота из угла при основании тр-ка (AH). ∠CEH = 75°.
CD — биссектриса, и высота и медиана, т.к. опущена из вершины на основание равнобедренного тр-ка.
Так как AH — высота, тогда ΔCEH — прямоугольный, ∠CHE = 90° (EH ∈ AH)
∠ECH = 90°−∠CEH = 90°−75° = 15°
∠A = ∠B = 90°−∠ECH = 90°−15° = 75° (т.к. ΔCBD — прямоугольный, ∠CDB = 90°).
ответ: угол при основании данного треугольника может быть равен 15° или 75°.