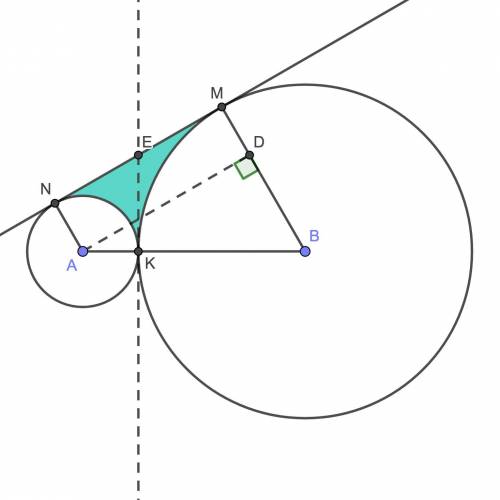
1) Отразим рисунок относительно прямой AB, окружности перейдут сами в себя, а K – перейдёт в точку K', симметричную относительно прямой AB. Если K не лежит на AB, то K и K' не совпадают, и K' – тоже точка касания, чего быть не может.
2) Радиусы, проведённые в точку касания, перпендикулярны касательной, поэтому AN и BM перпендикулярны NM, а тогда параллельны, ANMB – прямоугольная трапеция.
Проведём высоту трапеции AD. ANMD – прямоугольник, поэтому MD = AN = r, тогда BD = 2r. Кроме того, AB = AK + KB = 4r, поэтому ∠DAB = 30° (противолежащий катет равен половине гипотенузы), а по теореме Пифагора  .
.
Площадь трапеции ANMB равна 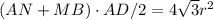
Площадь сектора KAN с центральным углом 90° + 30° = 120° = π/3 равна 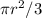
Площадь сектора KBM с центральным углом 90° - 30° = 60° = π/6 равна 
Площадь искомой фигуры
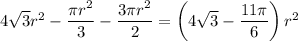
Пусть D - большая диагональ, а d - меньшая диагональ.
тогда d=D-14 см.
S=(1/2)*D*d или 120=(D-14)*D/2 или D²-14D-240=0.
D1=7+√(49+240)=7+17=24см.
D2=7-17=-10 - не удовлетворяет условию.
Итак, D=24см, а d=10см (24-14).
Диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам.
Тогда в прямоугольном треугольнике, образованном стороной ромба (гипотенуза) и половинами его диагоналей (катеты) по Пифагору найдем сторону ромба:
а=√((D/2)²+(d/2)²)=√(12²+5²)=√169 = 13см.
Периметр ромба равен 4*а=52см.
ответ.: Р=52см.