α = 60°
Объяснение:
Косинус угла между плоскостью треугольника и плоскостью его проекции равен отношению площади проекции (S₀) к площади треугольника (S):
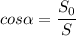
S = 48 см²
Площадь проекции найдем по формуле Герона:
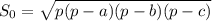
где р - полупериметр,
а, b и с - стороны треугольника.
a = 14 см, b = 16 cм, с = 6 см
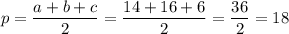 см
см
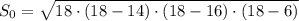
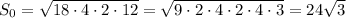 см²
см²
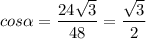
α = 60°
Теорема
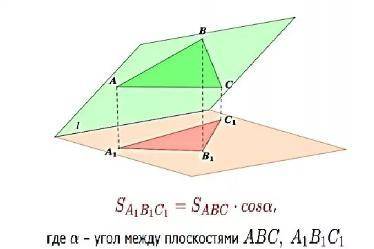
Площадь ортогональной проекции многоугольника на плоскости равна произведению его площади на косинус угла между плоскостью многоугольника и плоскостью проекции.см. картинку
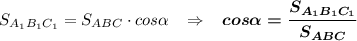
S abc = 48 см²
Найдем площадь треугольника А₁В₁С₁ по формуле Герона.
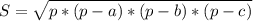
где 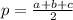 , a,b,c - стороны треугольника
, a,b,c - стороны треугольника
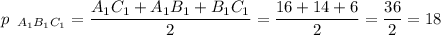
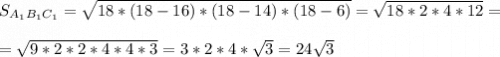
S a1b1c1 = 24√3 см²
Значит,
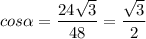
∠α = 60° - острый угол между данными плоскостями.
ответ: 60°
1. Прямые называют перпендикулярными, если они пересекаются под прямым углом (пример ниже).
2. Через одну точку на данную прямую можно опустить один перпендикуляр и только один. Если предположить, что можно провести, скажем, два перпендикуляра из заданной точки, то в получившемся треугольнике будет два прямых угла, что невозможно.
3. Градусная мера прямого угла = 90°.
4. Перпендикуляр — отрезок прямой, перпендикулярной данной, имеющий одним из своих концов точку их пересечения.
5. Наклонной, проведённой из данной точки к данной плоскости, называется любой отрезок, соединяющий данную точку с точкой плоскости, не являющийся перпендикуляром к плоскости.
6. Из точки А к прямой можно провести бесконечно много наклонных.

Ромб - это параллелограмм, у которого все стороны равны (докажите сами). То есть ромб является параллелограммом.
<AOE = <ACB (как соответственные углы при ||-ных прямых OE и BC и их секущей AC).
Тогда треугольники ACB и AOE подобны по двум углам (<A=<A, <AOE=<ACB),
тогда их стороны пропорциональны, то есть:
AC/AO = BC/EO = AB/AE. (*)
Треугольники AOB и COD равны (докажите сами), тогда
AO = CO, тогда
AC/AO = (AO+CO)/AO = 2AO/AO = 2.
Тогда из (*):
2 = BC/EO, отсюда EO = (1/2)*BC,
Но у ромба все стороны равны, то есть BC = DC, поэтому
EO = (1/2)*BC = (1/2)*DC.
Ч. т. д.
Чтобы найти угол необходимо найти площадь второго тр-ка.
Итак , сначала полупериметр 16+14+6=48/2=18.
Подставляем это число в формулу Герона , под большим корнем пишешь
18(18-14)(18-16)(18-6)=опять ккорень и под ним 2*9*4*2*4*3=24корень под ним 3.
теперь найдем угол по формуле S проекции= S * cos y
подставляем 24 корень из 3 * cos y = 48
cos y = 24 корень из 3 / 48 = дробью вверху корень из 3 , внизу 2 .
cos y = 30 гр.