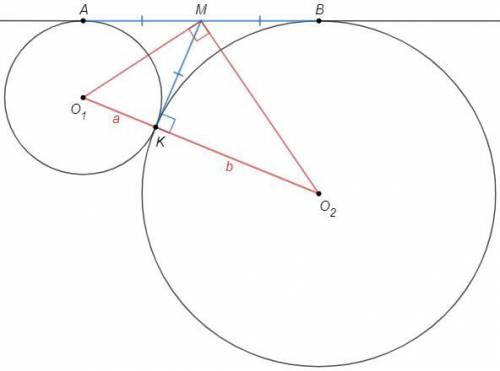
Рассмотрим две окружности, касающиеся внешним образом.
MK, AB - общие касательные
MA=MK=MB; MO1, MO2 - биссектрисы (т об отрезках касательных из одной точки)
∠O1MO2 =90 (биссектрисы смежных углов перпендикулярны)
∠MKO1 =90 (радиус в точку касания перпендикулярен касательной)
MK =√(O1K*O2K) =√(ab) (высота из прямого угла)
AB =2MK =2√(ab)
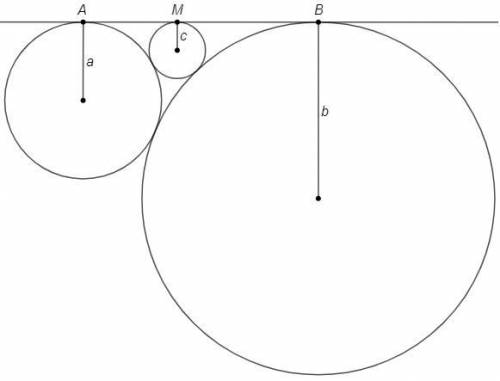
Теперь рассмотрим три окружности, для каждой пары выполняется предыдущее условие: касаются внешним образом и общей внешней касательной (c - меньший радиус).
AM =2√(ac)
BM =2√(bc)
AB =2√(ab) =AM+BM
=> √(ab) =√(ac) +√(bc) | :√(abc)
=> 1/√c = 1/√a + 1/√b
Два случая:
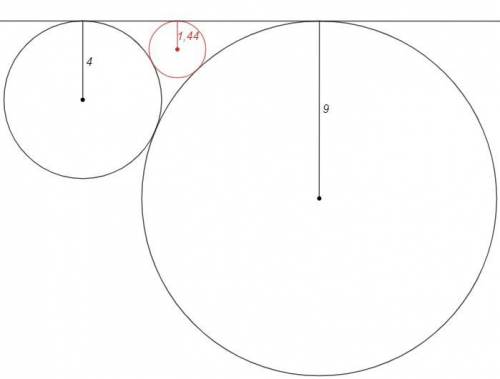
1) x - меньший радиус
1/√x =1/√4 +1/√9 => 1/√x =1/2 +1/3 =5/6 => x=36/25 =1,44
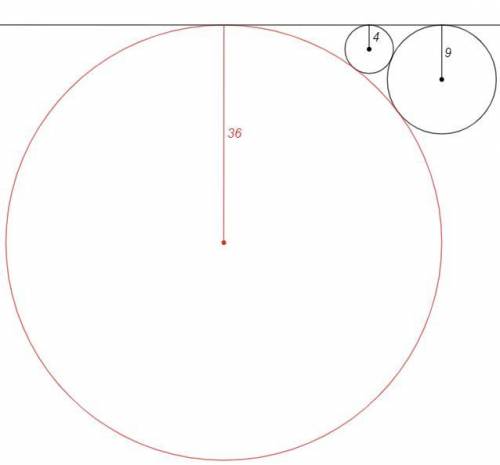
2) 4 - меньший радиус
1/√4 =1/√x +1/√9 => 1/√x =1/2 -1/3 =1/6 => x=36
Даны вершины треугольника A(1; 4); B(6; 5); C(4; -3).
Точка М = (B(6; 5) + C(4;-3)) / 2 = (4; 0,5).
Вектор АМ = М(4; 0,5) - A(-5; 1) = (9; -0,5).
Уравнение АМ: (x + 5) / 9 = (y - 1) / (-0,5) или в общем виде:
x + 18y - 13 = 0.
Высота BN перпендикулярна стороне АС.
Находим вектор АС = C(6; -3) - A(-5; 1) = (11; -4)
Уравнение АС: (x + 5) / 11 = (y - 1) / (-4) или в общем виде:
4x + 11y + 9 = 0.
Если к прямой Ax + By + C = 0 проведен перпендикуляр, то у него коэффициенты при переменных будут Bx - Ay.
Уравнение АС: 4x + 11y + 9 = 0.
Уравнение BN: 11x - 4y + C = 0. Для определения слагаемого С подставим координаты точки В, через которую проходит прямая BN.
11*2 - 4*4 + C = 0, отсюда С = 16 - 22 = -6.
Получаем уравнение BN: 11x - 4y - 6 = 0.
Находим угол:
Вектор АM Вектор ВN
х у х у
9 -0,5 11 -4
Модуль АM = 9,01387819 Модуль ВN = 11,7047
Угол между векторами
cos γ = 0,957303
γ = 0,293272 радиана
= 16,80328 градуса.
24/4=6 см Площадь ромба равна произведению основания на высоту,отсюда,S=30 S=аh 30=6h h=30/6=5 см