

ответ: 6√5 см
Объяснение:
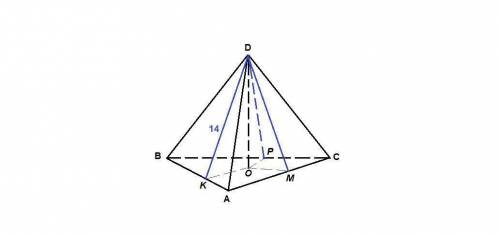
Пусть DO - высота пирамиды, DK, DM, DP - высоты боковых граней.
DK = DM = DP = 14 см по условию.
OK, OM и ОР - проекции наклонных, тогда они перпендикулярны сторонам треугольника АВС по теореме о трех перпендикулярах.
Если равны наклонные, проведенные из одной точки, то равны и их проекции, значит
ОК = ОМ = ОР, следовательно О - центр окружности, вписанной в ΔАВС, а ОК, ОМ и ОР - ее радиусы.
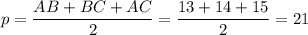
По формуле Герона
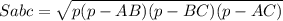
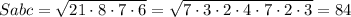 см²
см²
S = pr
84 = 21r
r = 4 см
ΔDKO: ∠DOK = 90°
по теореме Пифагора
DO = √(DK² - KO²) = √(196 - 16) = √180 = 6√5 см
Точки К и М - точки пересечения перпендикуляров а и b с осью пересечения плоскостей:
AK = a (на плоскость альфа)
BM = b (на плоскости бета)
KM = c (на линии пересечения плоскостей)
1) Треугольник AKM:
L AKM = 90 град.
AK = a
KM = c =>
AM^2 = AK^2 + KM^2 = a^2 + c^2 =>
AM = V(a^2 + c^2) - проекция АВ на плоскость альфа)
2) Треугольник ВМК:
L BMK = 90 град.
BM = b
KM = c =>
KB^2 = BM^2 + KM^2 = b^2 + c^2
КВ = V(b^2 + c^2) - проекция АВ на плоскость бета)
3) Треугольник АМВ:
L AMB = 90 град. (т. к. плоскости перпендикулярны =>прямые, принадлежащие плоскостям, перпендикулярны)
AM = V(a^2 + c^2)
BM = b =>
AB^2 = AM^2 + BM^2 = a^2 + c^2 + b^2
AB = V(a^2 + b^2 + c^2) - длина отрезка АВ.