60°,60°,60°.
Объяснение:
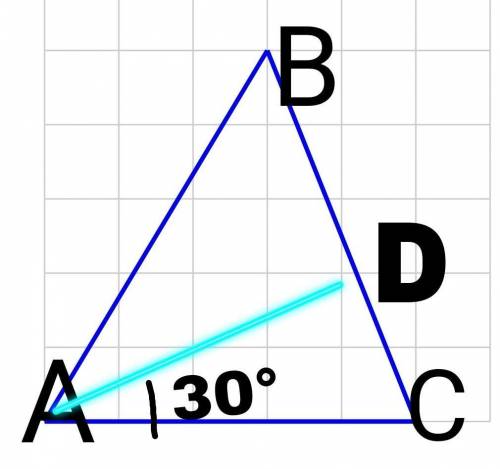
Так как в равнобедренном треугольнике высота является и биссектрисой, то АD - биссектриса, значит угол А = 30°+30°=60°. Так как АD - высота, то угол АDC=90°, следовательно, треугольник АDC-прямоугольный. Угол С=90°-30°=60°(сумма острых углов прямоугольного треугольника = 90°).
Угол В=180°-60°-60°=60°(сумма углов треугольника = 180°).
Либо же есть 2 вариант (попроще).
Находишь угол А=60°(по решению сверху), пишешь, что в равнобедренном треугольнике углы при основании равны, значит, угол А=углу С. А дальше находишь угол В, отнимая от 180° 120°, и получаешь 60°.
В тупоугольном треугольнике $ABC$ (см. рис. 1) две высоты ($AD$ и $BE)$ пересекают продолжение сторон и лежат вне треугольника; третья высота ($CF)$ пересекает сторону треугольника.В остроугольном треугольнике (рис. 2) все три высоты лежат внутри треугольника. В прямоугольном треугольнике катеты являются также и высотами. Три прямые, содержащие разные высоты треугольника, всегда пересекаются в одной точке, называемой ортоцентром треугольника. В тупоугольном треугольнике ортоцентр лежит вне треугольника; в остроугольном - внутри; в прямоугольном треугольнике ортоцентр совпадает с вершиной прямого угла. Высоты треугольника, опущенные на стороны
треугольника $a,b,c$ обозначаются $h_a ,h_b ,h_c $ соответственно.