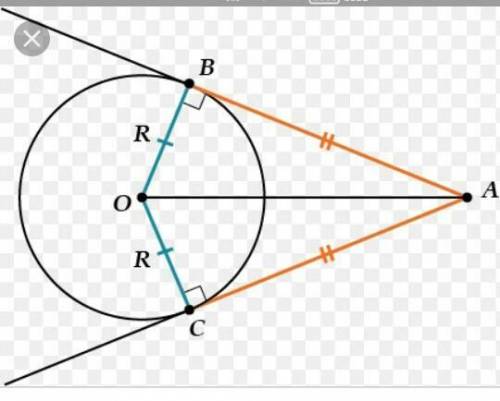
Дано: АВ и АС - касательные, ОА=30 см, ОВ=15 см.
Найти: угол ВОС.
Рассмотрим треуг-ки АОВ и АОС:
ОВ=ОС=R, ОА - общая, АВ=АС (по определению - отрезки касательных, проведенных из одной точки, равны) => эти треугольники равны по 3-му признаку=> уголВОА=угол ОСА.
Рассм. треуг. АОВ: т.к. ОВ в 2 раза меньше АО, то угол ОАВ=30 градусов(сторона, лежащая напротив угла в 30 градусов, равна половине гипотенузы). угол ВОА=180-90-30=60 градусов.
угол ВОС= угол ВОА+ угол ОСА= 60+60=120 градусов.
ответ: 120 градусов.
1) В четырехугольнике ABCD точки E и F — соответственно середины равных сторон AB и CD . Серединные перпендикуляр к стороне AD пересекает серединный перпендикуляр к стороне BC в точке P . Докажите, что серединный перпендикуляр, проведенный к отрезку EF проходит через точку P .
2) В четырехугольнике ABCD серединные перпендикуляры к сторонамAB и CD пересекаются на стороне AD . Известно, что \angle A = \angle D . Докажите, что в четырехугольнике диагонали равны.
3) В квадрате ABCD даны точки E и F соответственно на сторонах AB и BC ,причем \angle AED = \angle FED . Докажите равенство EF = AE + FC
так???!!!
произведение отрезков одной хорды равно произведению отрезков другой, т.е.
20*4=х*(х-2)
80=х^2-2x
x^2-2x-80=0
x1=10, x2=-8(не подходит по смыслу)
10 см один отрезок, 10-2=8 см второй отрезок.
Хорда равна 10+8=18 см.