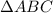
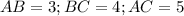
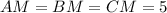
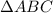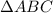. . Это - египетский прямоугольный треугольник, что подтверждается теоремой Пифагора: 
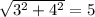. А центр описанной окружности прямоугольного треугольника лежит в середине гипотенузы. Итак, радиус этой окружности равен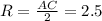 
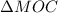. В нем 
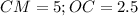. Третью сторону найдем по теореме Пифагора: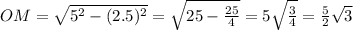
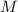до плоскости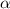 
есть такое свойство: квалрат длины катета прямоугольного треугольника равен произведению длины гипотенузы и длины проекции этого катета на гипотенузу. построй треугольник ABC (C=90) точка D - точка пересечения высоты, проведенной из прямого угла к гопотенузе. значит CB*CB=AB*DB отсюда следует, что DB=4
отнимаем от 25-4=21 получаем проекцию другого катета