Якщо ще актуально)
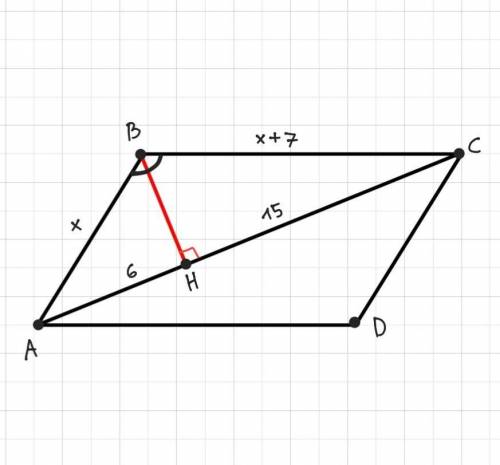
Дано: ABCD - паралелограм, АС - діагональ, ВН⟂АС, АН= 6 см, СН= 15 см, ВС–АВ= 7 см.
Знайти: S abcd.
Розв'язання.
Розглянемо трикутники АНВ і СНВ.
Вони прямокутні, а сторона ВН для них є спільним катетом. АН= 6 см, СН= 15 см, тому очевидно, що ВС>АВ.
Нехай АВ= х см, тоді ВС= (х+7) см.
Оскільки ВН - спільна сторона, тоді справедлива така рівність (через т.Піфагора у ΔAHB і ΔCHB):
АВ²–АН²= ВС²–НС²;
х²–6²= (х+7)²–15²;
х²–6²= х²+14х+49–225;
х²–х²–14х= 36+49–225;
–14х= –140;
14х= 140;
х= 10 (см)
Отже, АВ= 10 см, тоді:
ВН²= х²–6²= 10²–6²= 100–36= 64;
ВН= 8 см (–8 не може бути)
Розглянемо ΔABC:
AC= AH+HC= 6+15= 21 см
ВН= 8 см, ВН - висота ΔABC, оскільки ВН⟂АС.
Знайдемо площу ΔАВС:
S= ½•AC•BH;
S= ½•21•8= 84 (см²).
Діагоналі паралелограма ділять його на два рівних трикутники, тобто їх площі рівні.
SΔABC= SΔCDA= 84 см²
Звідси площа паралелограма ABCD дорівнює
S abcd= 2•SΔABC= 2•84= 168 (см²).
Відповідь: 168 см².
Объяснение:
Дано:
ABCD - параллелограмм.
AC и BD - диагонали параллелограмма.
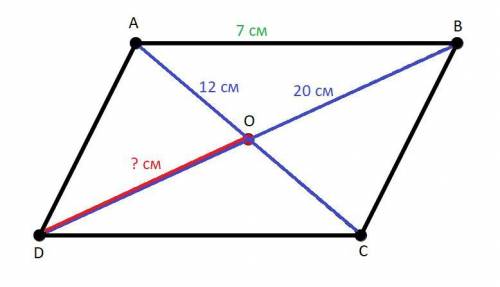
AC ∩ BD = O.
AC = 12 (см); BD = 20 (см); AB = 7 (см).
Найти:
DO - ? (см).
Тут всё довольно просто. Так как ABCD - параллелограмм, вспомним свойство такой геометрической фигуры: диагонали параллелограмма точкой пересечения делятся пополам. Т.е. диагонали AC и BD делятся точкой пересечения O пополам. Соответственно DO будет равняться половине всей диагонали BD. (и из этого следует, что DO = OB)
DO = BD/2 = 20 : 2 = 10 (см)
Докажем, что ABCD-параллелограм
угол ABC и BCD односторонние, т.к. AB || DC и секущая BC
в сумме дают 180 градусов, а значит угол ABC=180-DCB
углы CDA и DAB односторонние, т.к. AB || DC и секущая AD
в сумме дают 180 градусов, а значит угол ADC=180-DAB
из этого следует, что углы ABC=ADC
т.к. противолежащие углы равны, ABCD-параллелограм
у параллелограма протеволежащие стороны равны, значит AD=DC
что и следовалось доказать