обозначим призму АВСDА1В1С1D1
красным цветом обозначено боковое ребро призмы и равно оно 14 см
зеленым цветом обозначена высота проведенная из точки А в точку Н и состовляющая угол с плоскостью основания 90 градусов.
получается прямоугольный треугольник АА1Н с гипотенузой АА1. одна из теорем прямоугоьного треугольника гласит: катет лежащий против угла в 30 градусов равен половине гипотенузы. в нашем случае таким катетом является искомая высота АН и она равна 14/2=7см
P.S. я не художник((( простите((
S = 50 ед².
Объяснение:
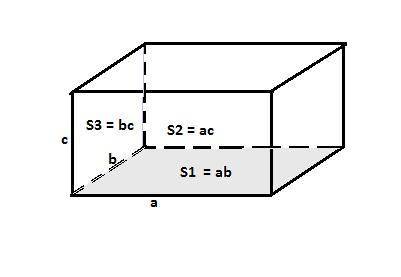
Пусть стороны прямоугольного параллелепипеда, образующие его измерения, равны "a", "b" и "c". Тогда площади основания и двух боковых граней равны
a·b = 48 (1), a·c = 40 (2) и b·c = 30 (3).
Выразим сторону b из равенств (1) и (3) и приравняем полученное:
b = 48/a и b = 30/c => 48/a = 30/c => c = 30a/48 = (5/8)a.
Подставим это значение в (2):
a·(5/8)a = 40 => a² = 320/5 = 64 => a = 8 ед.
Тогда из (1) b = 48/8 = 6 ед. c = 30/8 = 5 ед. (из 2).
Найдем по Пифагору диагональ основания:
d = √(a²+b²) = √(64+36) = 10 ед.
Площадь диагонального сечения равна:
S = d·c = 10·5 = 50 ед².
<A = <C = (180 - 36) : 2 = 72°
2. Угол А делится биссектрисой пополам, значит,
<DAC = 72 : 2 = 36°
3. Находим оставшийся неизвестный угол ADC в треугольнике ACD:
<ADC = 180 - 36 - 72 = 72°
Таким образом, <ADC = <C = 72°. Поскольку углы при основании DC в треугольнике ACD равны, значит он равнобедренный.