1) Найти радиус окружности.
МК = √((K(x) - M(x))² + (K(y) - M(y))²) = √((6 - 2)² + (3 - 3)²) = √16 = 4 ед.
Радиус окружности равен половине диаметра.
⇒ радиус окружности = МК/2 = 4/2 = 2 ед.
2) Найти координаты центра окружности.
Пусть О - центр окружности.
О(х) = (М(х) + К(х))/2 = (2 + 6)/2 = 4
О(у) = (М(у) + К(у))/2 = (3 + 3)/2 = 3
Итак, координаты О (4;3).
3) Написать уравнение окружности.
Уравнение окружности: (х - х₀)² + (у - у₀)² = R², где (х₀;у₀) - координаты центра окружности; (х;у) - координаты точки на окружности; R - радиус окружности.
⇒ уравнение данной окружности: (х - 4)² + (у - 3)² = 4
4) Окружность на картинке.
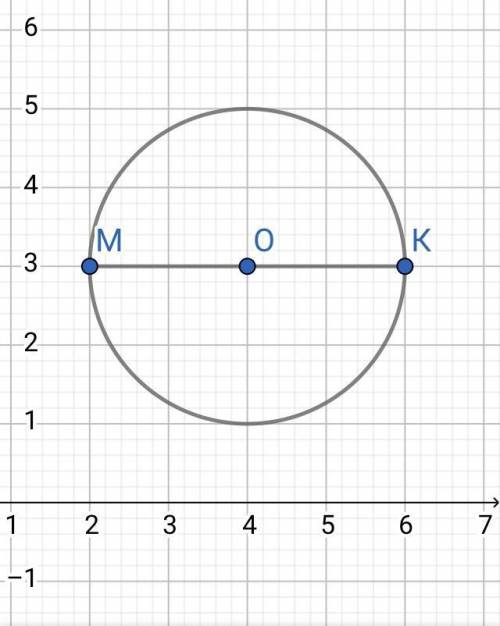
Объяснение:
*Рассчитаем длины сторон четырехугольника
IABI²=(1-4)² + (2-(-1))²=(-3)²+(3)²=9+9=18
IABI=√18
ICDI²=(5-8)²+(6-3)²=(-3)²+3²=9+9=18
ICDI=√18
IADI²=(5-1)²+(6-2)²=4²+4²=32
IADI=√32
IBCI²=(8-1)²+(3-(-1))²=4²+4²=16+16=32
IBCI=√32
стороны в четырехугольнике равны в парах
* рассчитываем длины диагонали
IACI²=(8-1)²+(3-2)²=7²+1²=49+1=50
IACI=√50
IBDI²=(5-4)²+(6-(-1))²=1²+7²=1+49=50
IBDI=√50
длины четырехугольных диагоналей равны
OTBET: если в четырехугольнике стороны равны попарно, а его диагонали равны, то это прямоугольник, который должен быть показан
Решение: Пусть ABCD – данный паралелограмм, BK-перпендикуляр, проведенный к диагонале AC, тогда
AC=AK+KС=6+15=21 cм.
Обозначим AB=x см, тога по условию BC=x+7 см.
По теореме Пифагора
BK=корень(AB^2-AK^2)= корень(BC^2-CK^2), получаем уравнение
корень(х^2-6^2)= корень((х+7)^2-15^2)
Поднеся к квадрату обе части уравнения, получим:
х^2-6^2= (х+7)^2-15^2. Решаем уравнение:
х^2-36-х^2-14x-49+225=0
50x=140
x=140\50=2.8
x+7=2.8+7=9.8
Значит AB=CD=2.8, BC=AD=9.8
Сумма квадратов диагоналей параллелограмма равна сумме квадратов сторон, поэтому
AC^2+BD^2=2*(AB^2+BC^2)
21^2+BD^2=2*(2.8^2+9.8^2), откуда
ВD=корень(233.24)=1.4*корень(119) см
ответ 2.8 см, 9.8 см – длины сторон,
21 см, 1.4*корень(119) см - длины диагоналей