У правильной четырёхугольной пирамиды в основании лежит квадрат, а основание высота пирамиды является центром квадрата. Зная сторону квадрата (l) можно найти его диагональ - 10√2. Найдём высоту (в одном из 4 треугольников, которые образуются при пересечении диагоналей квадрата) из середины квадрата:
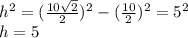
В принципе это и так логично, ведь диагональ квадрата составляет 45° с его сторонами. Теперь мы можем найти апофему пирамиды (её основание будет совпадать с основание недавно проведённой высоты т.к. это высота и медиана в равнобедренном треугольнике)
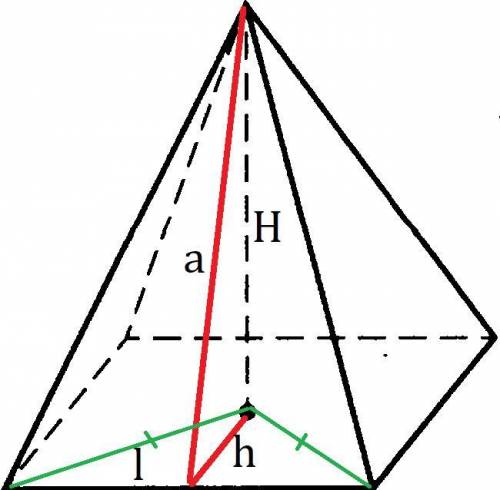
a - апофема (высота боковой грани).
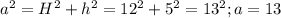
Пирамида правильная, поэтому все боковые грани равные треугольники, найдём площадь.
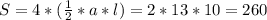
l - сторона основания.
ответ: 260 см².
"египетский" треугольник, подобный (3,4,5). Стороны 9,12,15. Расстояние от основания медианы к гипотенузе (то есть от середины гипотенузы) до катета 12 равно 9/2. А точка пересечения медиан на треть медианы ближе к вершине перяого угла, то есть расстояние от неё до катета 12 составит (2/3)*(9/2) = 3.
А можно и так. Медиана к гипотенузе равна 15/2, а точка пересечения медиан лежит на расстоянии (2/3)*(15/2) = 5 от прямого угла. При этом, если опустить перпендикуляр из этой точки на катет (да любой :)) в данном случае - на катет 12), то поучится ОПЯТЬ "египетский" треугольник, причем самый настоящий - (3,4,5). Доказательство этого совершенно очевидного факта такое - медиана образует с катетами углы, равные углам треугольника, поскольку разбивает треугольник на два равнобедренных. Отсюда следует подобие построенного треугольника исходному.
Ну, вот так само собой и получилось, что расстояние от точки пересечения медиан до катетов 3 и 4. Нужное по задаче расстояние 3.