∠С=30°,∠А=90°,∠В=60°
Объяснение:
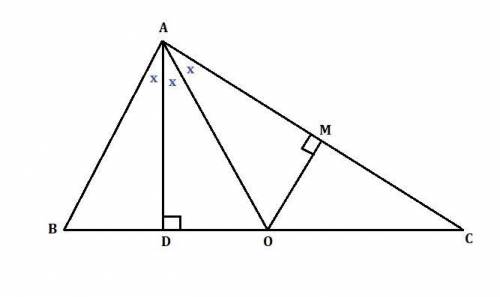
Дано: AD⊥BC, ВО=ОС. ∠ВАD=∠DАО=∠ОАС
Найти: ∠А,∠В,∠С ΔАВС
Пусть ∠ВАD=∠DАО=∠ОАС=х
1) Рассмотрим ΔВАО. АD - высота. ∠ВАD=∠DАО ⇒ АD - биссектриса.
Если в треугольнике медиана совпадает с биссектрисой, то треугольник равнобедренный. ⇒ΔВАО - равнобедренный. В равнобедренном треугольнике высота является также медианой. ⇒
ВD=DО=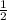 
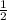ВО= ОС.
2) Дополнительное построение: Проведём ОМ⊥АС.
Рассмотрим прямоугольные треугольники АDО и АМО.
∠DАО=∠ОАС - по условию, АО - общая.
Если гипотенуза и острый угол одного треугольника соответственно равны гипотенузе и острому углу другого треугольника, то такие прямоугольные треугольники равны.⇒ΔАDО = ΔАМО
Из равенства треугольников следует равенство катетов:
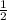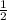DО = МО = ВО= ОС.
3) Рассмотрим прямоугольный треугольник ОМС (∠М=90°).
Из доказанного выше МО=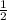ОС. Т.е. катет МО равен половине гипотенузы ОС.
Следовательно ∠С=30°
4) Рассмотрим прямоугольный треугольник АDC(∠D=90°).
По свойству острых углов прямоугольного треугольника
∠DАС=90°-∠С=90°-30°=60°.
По условию ∠DАС=2х ⇒ 2х=60°, х=30°
5) ∠ВАС=3х=3*30°=90°
∠А треугольника АВС = 90°
Так как сумма углов треугольника равна 180°, то ∠В треугольника АВС будет равен: ∠В=180°-∠А-∠С=180°-90°-30°=60°
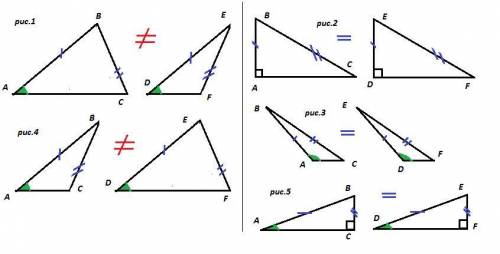
Первый признак равенства треугольников : по двум равным сторонам и равному углу между ними. В условии равные углы не образованы равными сторонами. Утверждать, что треугольники равны, нельзя (рис.1).
2. ∠BAC — прямой: ∠BAC = ∠EDF = 90°; (рис.2)
AB=DE (равные катеты); BC=EF (равные гипотенузы) ⇒
ΔABC = ΔDEF по равным катету и гипотенузе.
3. ∠BAC — тупой : ∠BAC = ∠EDF > 90°; (рис.3)
Так как в треугольнике может быть только один тупой угол, а два других будут острыми, то по теореме синусов
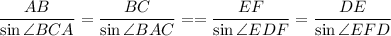
AB=DE ⇒ sin∠BCA = sin∠EFD ⇒ ∠BCA = ∠EFD (оба острые)
⇒ ∠ABC = ∠DEF (по сумме углов треугольника) ⇒
ΔABC = ΔDEF по двум равным сторонам и углу между ними.
5. ∠BCA — прямой : Так как в треугольнике может быть только один прямой угол, а два других будут острыми, то по теореме синусов
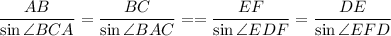
AB=DE ⇒ sin∠BCA = sin∠EFD ⇒ ∠BCA = ∠EFD = 90°
ΔABC = ΔDEF по равным катету и гипотенузе.
=====================================
Остальные дополнительные условия недостаточны - видно на рисунках.
1. ∠BAC — острый - рис.1
4. ∠BCA — острый - рис.1
6. ∠BCA — тупой - рис.4
7. AB>BC — рис.1, рис.4
